
创建自己的小题库
搜索

等比数列的定义及性质题库
题数
2000
考试分类
高中数学>等比数列的定义及性质
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-等比数列的定义及性质
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]已知等比数列 【图片】的公比为正数,且 【图片】, 【图片】,则 【图片】( ) A. 【图片】B. 【图片】C. 【图片】D....
参考答案:
|
B
|
参考解析:
等比数列
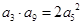 中,
中,
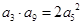 既是
既是
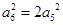
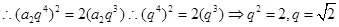 ,
,
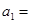
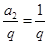 =
=
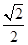 。
。
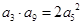 中,
中,
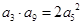 既是
既是
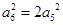
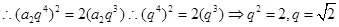 ,
,
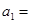
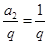 =
=
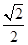 。
。
【简答题】

[2/2000]已知 【图片】是首项为 【图片】的等比数列, 【图片】是 【图片】的前 【图片】项和,且 【图片】.则 【图片】的前 【图片】项和为. A. 【图片】...
参考答案:
|
C
|
参考解析:
解:∵等比数列前n项和公式 Sn=
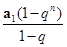 ,而9S
3=S
6,∴列等式可知q=2,所以a
1=1,a
2=2,a
3=4…其倒数列前五项为
,而9S
3=S
6,∴列等式可知q=2,所以a
1=1,a
2=2,a
3=4…其倒数列前五项为
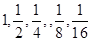 故前5项和为
故前5项和为
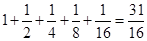 ,故选C.
,故选C.
点评:本题主要考查数列的求和和等比数列的性质的知识点,解答本题的关键是求出等比数列的公比,本题难度不是很大.
【简答题】

[3/2000]在等比数列 【图片】中,若 【图片】, 则 【图片】的值为( ) A. 【图片】B. 【图片】C. 【图片】D. 【...
参考答案:
|
C
|
参考解析:
由
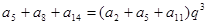 ,可得
,可得
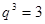 ,则
,则
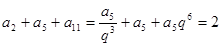 ,解得
,解得
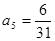 ,所以
,所以
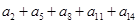
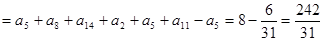 .
.
【简答题】

[4/2000]已知数列{an}满足a1=2,10a n+1﹣9an﹣1=0, 【图片】 .(1)求证:数列{an﹣1}是等比数列;(2)当n取何值时,bn...
参考答案:
| (1)证明:∵a10an+1﹣9an﹣1=0, ∴  . . ∴  , ,∵a1=2, ∴{an﹣1}是以a1﹣1=1为首项,公比为  的等比数列. 的等比数列.(2)解:由( 1),可知an﹣1=  (n∈N*). ∴ (n∈N*). ∴ , , .当n=7时, .当n=7时,  ,b8=b7; ,b8=b7;当n<7时,  ,bn+1>bn; ,bn+1>bn;当n>7时,  ,bn+1<bn. ,bn+1<bn. ∴当n=7或n=8时,bn取最大值,最大值为  . .(3)解:由  ,得 ,得 .(*) .(*)依题意,(*)式对任意m∈N*恒成立, ①当t=0时,(*)式显然不成立,因此t=0不合题意. ②当t<0时,由  ,可知tm<0(m∈N*),而当m是偶数时tm>0,因此t<0不合题意. ,可知tm<0(m∈N*),而当m是偶数时tm>0,因此t<0不合题意.③当t>0时,由tm>0(m∈N*), ∴  ,∴ ,∴  (m∈N*). (m∈N*).设  (m∈N*), ∵ (m∈N*), ∵  = = , , ∴h(1)>h(2)>…>h(m﹣1)>h(m)>…. ∴h(m)的最大值为  . .所以实数t的取值范围是  . . |
参考解析:
无
【简答题】

[5/2000].已知等比数列 【图片】中,且 【图片】, 【图片】,求公比 【图片】,通项公式 【图片】及前 【图片】项和 【图片】.
参考答案:
|
解:
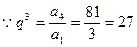

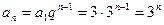
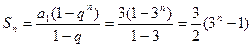 . .
|
参考解析:
无
【简答题】

[6/2000]对于数列 【图片】,定义 【图片】为数列 【图片】的一阶差分数列,其中 【图片】;对 【图片】,定义 【图片】为 【图片】的 【图片】阶差分数列,其中...
参考答案:
|
(略)
|
参考解析:
(1)
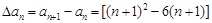
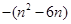 =
=
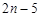 。
。
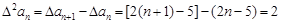 。
。
(2)由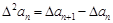 与
与
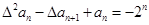 得
得
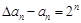 ,所以
,所以
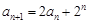
所以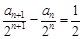 ,则
,则
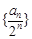 是等差数列。
是等差数列。
所以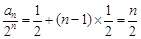 ,所以
,所以
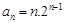 。
。
所以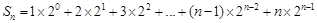 ①
①
则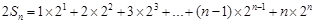 ②
②
由①-②得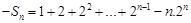
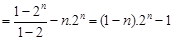
所以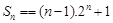
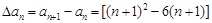
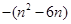 =
=
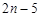 。
。
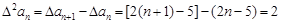 。
。
(2)由
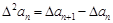 与
与
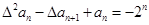 得
得
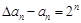 ,所以
,所以
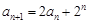
所以
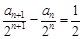 ,则
,则
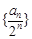 是等差数列。
是等差数列。
所以
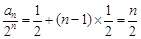 ,所以
,所以
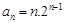 。
。
所以
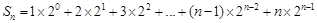 ①
①
则
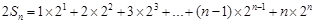 ②
②
由①-②得
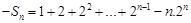
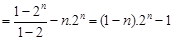
所以
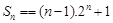
【简答题】

[7/2000]设 【图片】为等比数列, 【图片】为其前 【图片】项和,已知 【图片】. (1)求 【图片】的通项公式; (2)求数列 【图片】的前 【图片】项和 【...
参考答案:
|
(1)
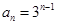 ;(2) ;(2)

|
参考解析:
(1)由
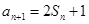 ,得
,得
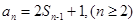 ,然后两式相减得等比数列的公比q,然后根据已知递推公式可求得
,然后两式相减得等比数列的公比q,然后根据已知递推公式可求得
 ,从而可求得
,从而可求得
 的通项公式;(2)考虑利用错位相减示求数列
的通项公式;(2)考虑利用错位相减示求数列
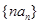 的前
的前
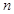 项和
项和
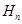 .
.
(1)
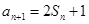 ,
,
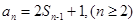 ,
,
∴
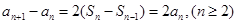 ,
,
∴
 ,
,
∴
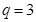 ,
,
对于
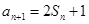 令
令
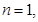 可得
可得
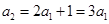 ,解得
,解得
 ,
,
∴
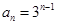 .
.
(2)
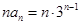 ,
,
 ①,
①,
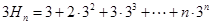 ② ,
② ,
①-②得
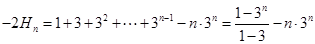 ,
,
∴
 .
.
【简答题】

[8/2000]已知等差数列{an}中,a1=-1,前12项和S12=186.(Ⅰ)求数列{an}的通项公式;(Ⅱ)若数列{bn}满足bn=( 12)an,记数列{b...
参考答案:
| (Ⅰ)设等差数列{an}的公差为d,∵a1=-1,S12=186, ∴S12=12a1+
所以数列{an}的通项公式an=-1+(n-1)×3=3n-4. (Ⅱ)∵bn=(
∵当n≥2时,
∴数列f(1)=
∴Tn=
∵
而1-(
∴m≥
|
参考解析:
12×112
【简答题】

[9/2000]等比数列{an}中,an>0,且a4a6+2a5a7+a6a8=36,则a5+a7的值为 [ ] A....
参考答案:
| A |
参考解析:
无
【简答题】

[10/2000]设正项等比数列 【图片】, 【图片】成等差数列,公差 【图片】,且 【图片】的前三项和为 【图片】,则 【图片】的通项为 A. 【图片】B. 【图片】...
参考答案:
|
B
|
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





