
创建自己的小题库
搜索

柯西不等式题库
题数
98
考试分类
高中数学>柯西不等式
售价
¥10
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-柯西不等式
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/98]已知a,b,c∈R+,且a+b+c=1,求3a+1+ 3b+1+ 3c+1的最大值.
参考答案:
| 根据柯西不等式,可得 (
=(1?
≤(12+12+12)[(
当且仅当
即a=b=c=
因此,
|
参考解析:
3a+1
【简答题】

[2/98](2013•湖北)设x,y,z∈R,且满足: 【图片】,则x+y+z= _________ .
参考答案:

|
参考解析:
根据柯西不等式,得
(x+2y+3z) 2≤(1 2+2 2+3 2)(x 2+y 2+z 2)=14(x 2+y 2+z 2)
当且仅当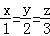 时,上式的等号成立
时,上式的等号成立
∵x 2+y 2+z 2=1,∴(x+2y+3z) 2≤14,
结合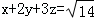 ,可得x+2y+3z恰好取到最大值
,可得x+2y+3z恰好取到最大值
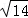
∴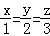 =
=
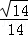 ,可得x=
,可得x=
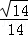 ,y=
,y=
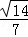 ,z=
,z=
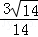
因此,x+y+z=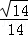 +
+
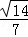 +
+
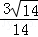 =
=

故答案为:
(x+2y+3z) 2≤(1 2+2 2+3 2)(x 2+y 2+z 2)=14(x 2+y 2+z 2)
当且仅当
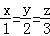 时,上式的等号成立
时,上式的等号成立
∵x 2+y 2+z 2=1,∴(x+2y+3z) 2≤14,
结合
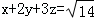 ,可得x+2y+3z恰好取到最大值
,可得x+2y+3z恰好取到最大值
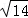
∴
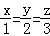 =
=
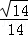 ,可得x=
,可得x=
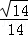 ,y=
,y=
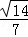 ,z=
,z=
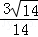
因此,x+y+z=
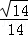 +
+
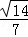 +
+
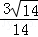 =
=

故答案为:

【简答题】

[3/98]若实数a,b,c,d满足:a+b+c+d=3,a2+2b2+3c2+6d2=5,则a的最大值是( )。
参考答案:
| 2 |
参考解析:
无
【简答题】

[4/98](选做题)设a,b,c均为正实数.(1)若a+b+c=1,求a2+b2+c2的最小值;(2)求证: 【图片】. 【图片】
参考答案:
| 解:(1)因为a,b,c 均为正实数,由柯西不等式得, (a2+b2+c2)(12+12+12)≥(a+b+c)2=1,当且仅当a=b=c=  时等号成立, 时等号成立,∴a2+b2+c2 的最小值为  . . (2)∵a,b,c均为正实数, ∴可得  ( (  + + )≥ )≥  ≥ ≥  , ,同理  ( (  + + )≥ )≥  , ,  ( (  + +  )≥ )≥  , ,三个不等式相加得  , ,当且仅当a=b=c时等号成立. |
 |
参考解析:
无
【简答题】

[5/98]选修4—5;不等式选讲 已知f(x)=x|x-a|-2 (1)当a=1时,解不等式f(x)<|x-2| (2)当x∈(0,1]时,f(x)<...
参考答案:


|
参考解析:
无
【简答题】

[6/98]已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5,求a的取值范围.
参考答案:
由柯西不等式得(
即2b2+3c2+6d2≥(b+c+d)2 将条件代入可得5-a2≥(3-a)2,解得1≤a≤2 当且仅当
可知b=
b=1,c=
所以:a的取值范围是[1,2]. |
参考解析:
无
【简答题】

[7/98](不等式选讲选做题)设 x+ y+ z=2,则 m= x2+2 y2+ z2的最小值为_______
参考答案:
|
8
|
参考解析:
考查了不等式的求最值
【简答题】

[8/98]D.选修4—5:不等式选讲 (本小题满分10分) 求函数 【图片】的最大值.
参考答案:
|
. 因为
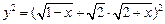 ≤ ≤
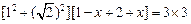 ………6分 ………6分
∴ 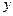 ≤ ≤
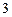 …8分, …8分,
当且仅当 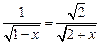 时取 时取
 “ “
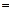 ”号,即当 ”号,即当
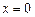 时, 时,
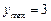 ………10 ………10
 分 分
|
参考解析:
略
【简答题】

[9/98](本大题9分)已知大于1的正数 【图片】满足 【图片】(1)求证: 【图片】(2)求 【图片】的最小值.
参考答案:
|
(1)见解析;(2)3.
|
参考解析:
(1)根据柯西不等式证明即可.
(2)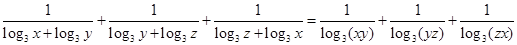
然后再根据柯西不等式证明即可.
证明:(1)由柯西不等式得:
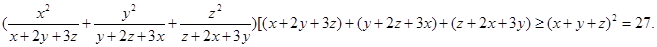 得:
得:
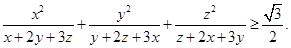
(2)
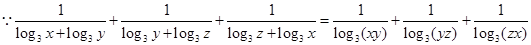
由柯西不等式得: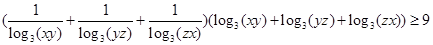 ,所以,
,所以,
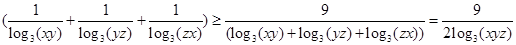
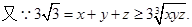
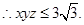
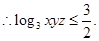 得
得
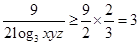
所以,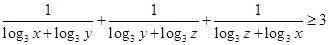 当且仅当
当且仅当
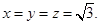 时,等号成立.故所求的最小值是3.
时,等号成立.故所求的最小值是3.
(2)
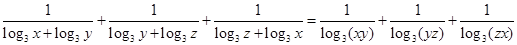
然后再根据柯西不等式证明即可.
证明:(1)由柯西不等式得:
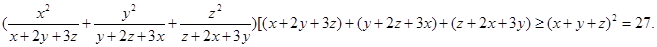 得:
得:
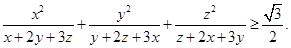
(2)
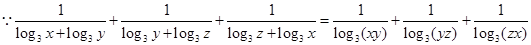
由柯西不等式得:
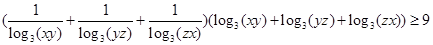 ,所以,
,所以,
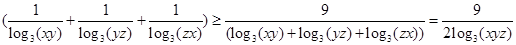
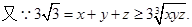
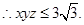
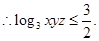 得
得
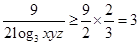
所以,
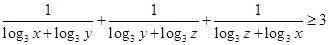 当且仅当
当且仅当
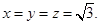 时,等号成立.故所求的最小值是3.
时,等号成立.故所求的最小值是3.
【简答题】

[10/98]设α,β,γ 都是锐角,且sinα+sinβ+sinγ=1,证明(1)sin2α+sin2β+sin2γ≥13;(2)tan2α+tan2β...
参考答案:
| 证明:(1)由柯西不等式得:(sin2α+sin2β+sin2γ)(1+1+1)≥(1•sinα+1•sinβ+1•sinγ)2, 因为sinα+sinβ+sinγ=1,所以3(sin2α+sin2β+sin2γ)≥1,得:sin2α+sin2β+sin2γ≥
(2)由恒等式tan2x=
得tan2α+tan2β+tan2 γ=
于是
由此得tan2α+tan2β+tan2 γ≥
|
参考解析:
13

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





