
创建自己的小题库
搜索

平面向量的应用题库
题数
1403
考试分类
高中数学>平面向量的应用
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-平面向量的应用
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1403]在△ABC中,若AB=1,AC= 【图片】,| 【图片】+ 【图片】|=| 【图片】|,则 【图片】=________.
参考答案:
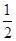
|
参考解析:
易知满足|
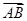 +
+
 |=|
|=|
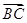 |的A、B、C构成直角三角形的三个顶点,且∠A为直角,于是
|的A、B、C构成直角三角形的三个顶点,且∠A为直角,于是
 =|
=|
 |·cos∠ABC=1×cos60°=
|·cos∠ABC=1×cos60°=
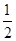 .
.
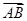 +
+
 |=|
|=|
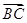 |的A、B、C构成直角三角形的三个顶点,且∠A为直角,于是
|的A、B、C构成直角三角形的三个顶点,且∠A为直角,于是
 =|
=|
 |·cos∠ABC=1×cos60°=
|·cos∠ABC=1×cos60°=
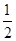 .
.
【简答题】

[2/1403]设F1、F2分别是椭圆x24+y2=1的左、右焦点,B(0,-1).(Ⅰ)若P是该椭圆上的一个动点,求PF1• PF2的最大值和最小值;(Ⅱ)若C为椭...
参考答案:
(Ⅰ)易知a=2,b=1,c=
设P(x,y),则
=x2+1-
因为x∈[-2,2],故当x=0,即点P为椭圆短轴端点时,
当x=±2,即点P为椭圆长轴端点时,
(Ⅱ)设C(x0,y0),B(0,-1),F1(-
又
(Ⅲ) 因为|PF1|+|PB|=4-|PF2|+|PB|≤4+|BF2|,∴△PBF1的周长≤4+|BF2|+|BF1|≤8. 所以当P点位于直线BF2与椭圆的交点处时,△PBF1周长最大,最大值为8. |
参考解析:
3
【简答题】

[3/1403]已知 【图片】. (Ⅰ)求 【图片】的夹角 【图片】; (Ⅱ)求向...
参考答案:
|
(Ⅰ)
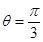 (Ⅱ) (Ⅱ)
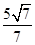
|
参考解析:
(I)由
 得
得
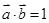 ,
,
再根据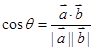 求角即可.
求角即可.
 , 即
, 即
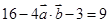
∴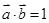 ∴
∴
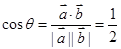
∵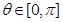 ∴
∴
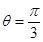
(2)先求出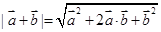 ,然后根据向量
,然后根据向量
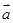 在
在
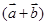 上的投影等于
上的投影等于
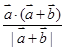 求值.
求值.
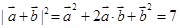
∴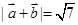 ,设
,设
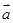 与
与
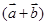 的夹角为
的夹角为
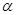
∴向量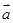 在
在
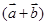 上的投影为
上的投影为
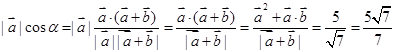
 得
得
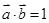 ,
,
再根据
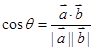 求角即可.
求角即可.
 , 即
, 即
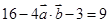
∴
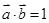 ∴
∴
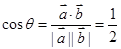
∵
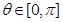 ∴
∴
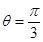
(2)先求出
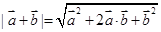 ,然后根据向量
,然后根据向量
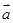 在
在
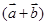 上的投影等于
上的投影等于
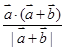 求值.
求值.
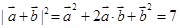
∴
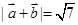 ,设
,设
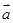 与
与
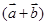 的夹角为
的夹角为
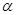
∴向量
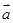 在
在
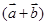 上的投影为
上的投影为
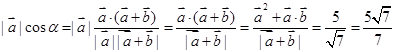
【简答题】

[4/1403]设 【图片】是锐角 【图片】的两内角, 【图片】,则 【图片】与 【图片】的夹角是( ) ...
参考答案:
|
B
|
参考解析:
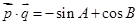 .因为
.因为
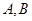 是锐角
是锐角
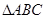 的两内角,所以
的两内角,所以
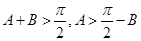 ,所以
,所以
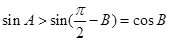 ,即
,即
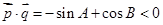 ,所以
,所以
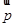 与
与
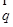 的夹角是钝角.
的夹角是钝角.
【简答题】

[5/1403]定义a* b是向量a和b的“向量积”,它的长度| a* b|=| a|•| b|•sinθ,其中θ为向量a和b的夹角,若u=(2,0), v=(1, ...
参考答案:
∵
∴
设
则cosθ=
∴|
故选B. |
参考解析:
u
【简答题】

[6/1403]已知 【图片】, 【图片】, 【图片】为坐标原点,点C在∠AOB内,且 【图片】,设 【图片】,则 【图片】的值为( ...
参考答案:
|
C.
|
参考解析:
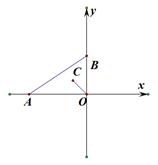
如图所示,∵
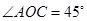 ,∴设
,∴设
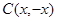 ,
,
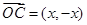 ,又∵
,又∵
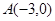 ,
,
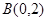 ,
,
∴
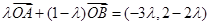 ,∴
,∴
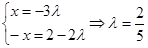 .
.
【简答题】

[7/1403]设D为△ABC的边AB上一点,P为△ABC内一点,且满足: 【图片】, 【图片】 【图片】,则 【图片】= &nb...
参考答案:
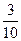
|
参考解析:
略
【简答题】

[8/1403]已知直线l1:x-2y+3=0,l2过点(1,1),并且它们的方向向量a1, a2满足a1• a2=0,那么l2的方程是______.
参考答案:
由题意,直线l1:x-2y+3=0的斜率为
又两直线的方向向量
∴两直线垂直,故直线l2的斜率为-2 又l2过点(1,1), ∴l2的方程是y-1=-2(x-1),整理得2x+y-3=0 故答案为2x+y-3=0 |
参考解析:
12
【简答题】

[9/1403]已知P为ΔABC所在平面内一点,若 【图片】,则点P轨迹过ΔABC的( ) A.内心B.垂心C.外心D.重心
参考答案:
|
D
|
参考解析:
略
【简答题】

[10/1403](本小题满分14分) 【图片】已知向量 【图片】与向量 【图片】的对应关系可用 【图片】表示.试问是否存在向量 【图片】,使得 【图片】成立?如果存在...
参考答案:
|
解:设存在向量
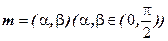 ,使得 ,使得
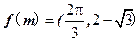 成立, ………………2分 成立, ………………2分
所以 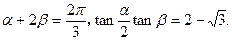 ………………① ……5分 ………………① ……5分
所以 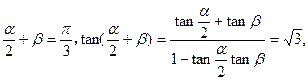
结合①,得 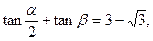 ………………② ………8分 ………………② ………8分
解①②组成的方程组得, 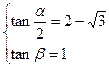 或 或
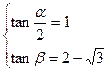 (舍去) …………11分 (舍去) …………11分
所以 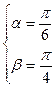 ,符合题意,假设成立, …………………………13分 ,符合题意,假设成立, …………………………13分
所以存在向量 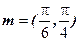 . …………………………14分 . …………………………14分
|
参考解析:
略

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





