创建自己的小题库
搜索
众数、中位数、平均数题库
题数
336
考试分类
高中数学>众数、中位数、平均数
售价
¥20
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-众数、中位数、平均数
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/336]甲、乙两名篮球运动员在某几场比赛得分的茎叶图如图所示，则甲、乙两人这几场比赛得分的中位数之和是 【图片】 [ &nb...
参考答案：
| A |
参考解析：
无
【简答题】
[2/336]一位同学用计算器求30个数据的平均数时，错将其中一个数据15输入为105，那么由此求出的平均数与实际平均数的差是（ ） A．3 B．3.5 C．4 ...
参考答案：
| A |
参考解析：
无
【简答题】
[3/336]已知总体的各个体的值由小到大依次为2，3，3，7，a，b，12，13.7，18.3，20，且总体的中位数为10.5，若要使该总体的方差最小，则a、b的...
参考答案：
 |
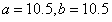参考解析：
无
【简答题】
[4/336]奥运会体操比赛的计分规则为：当评委亮分后，其成绩先去掉一个最高分，去掉一个最低分，再计算剩下分数的平均值，这是因为 A．减少计算量 B．避免故障 C．...
参考答案：
| C |
参考解析：
无
【简答题】
[5/336]同学们都知道，在一次考试后，如果按顺序去掉一些高分，那么班级的平均分将降低；反之，如果按顺序去掉一些低分，那么班级的平均分将提高．这两个事实可以用数学...
参考答案：
 和 |
参考解析：
无
【简答题】
[6/336]与原数据单位不一样的是（ ） A．众数 B．平均数 C．标准差 D．方差
参考答案：
| D |
参考解析：
无
【简答题】
[7/336]以下茎叶图记录了甲、乙两组个四名同学的植树棵树。乙组记录中有一个数据模糊，无法确认，在图中以X表示。 【图片】 （Ⅰ）如果X=8，求乙组同学植树棵树的...
参考答案：
| 解：（1）当X=8时，由茎叶图可知， 乙组同学的植树棵数是：8，8，9，10， 所以平均数为  ，方差为  。（Ⅱ）当X=9时，由茎叶图可知，甲组同学的植树棵树是：9，9，11，11； 乙组同学的植树棵数是：9，8，9，10。 分别从甲、乙两组中随机选取一名同学，共有4×4=16种可能的结果， 这两名同学植树总棵数Y的可能取值为17，18，19，20，21， 事件“Y=17”等价于“甲组选出的同学植树9棵，乙组选出的同学植树8棵”， 所以该事件有2种可能的结果，因此P（Y=17）=  ，同理可得  ， ，所以随机变量Y的分布列为：
=17×  +18× +19×+20× +21× =19。
|
参考解析：
Y
17
18
19
20
21
P
【简答题】
[8/336]某班进行个人投篮比赛，受污损的下表记录了在规定时间内投进n个球的人数分布情况： 进球数n 0 &nbs...
参考答案：
设投进3个球和4个球的各有x，y人，则
答：投进3个球和4个球的分别有12人和6人． |
参考解析：
|
||
|
【简答题】
[9/336]在测量某物理量的过程中，因仪器和观察的误差，使得n次测量分别得到a1，a2，…，an，共n个数据．我们规定所测量的“量佳近似值”a是这样一个量：与其他...
参考答案：
| ∵所测量的“量佳近似值”a是与其他近似值比较， a与各数据的差的平方和最小． 根据均值不等式求平方和的最小值知这些数的底数要尽可能的接近， ∴a是所有数字的平均数， ∴a=
故答案为：
|
参考解析：
无
【简答题】
[10/336]如图是一个容量为200的样本的频率分布直方图，根据图中数据填空：（1）样本数据落在范围[9，13）的频数为（ &nb...
参考答案：
| 72；10.52；11；13． |
参考解析：
无
