
创建自己的小题库
搜索

正弦定理题库
题数
2000
考试分类
高中数学>正弦定理
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-正弦定理
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]若(a+b+c)(b+c-a)=3bc,且sinA="2sinBcosC," 那么ΔABC是( ) A.直角三角形B...
参考答案:
|
D
|
参考解析:
因为(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,
解:∵(a+b+c)(b+c-a)=3bc∴[(b+c)+a][(b+c)-a]=3bc∴(b+c) 2-a 2=3bc
b 2+2bc+c 2-a 2=3bc,b 2-bc+c 2=a 2
根据余弦定理有a 2=b 2+c 2-2bccosA
∴b 2-bc+c 2=a 2=b 2+c 2-2bccosA
bc=2bccosAcosA=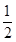 ∴A=60°又由sinA=2sinBcosC,
∴A=60°又由sinA=2sinBcosC,
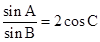 ,解得b=c,故三角形为.等边三角形,选D
,解得b=c,故三角形为.等边三角形,选D
解:∵(a+b+c)(b+c-a)=3bc∴[(b+c)+a][(b+c)-a]=3bc∴(b+c) 2-a 2=3bc
b 2+2bc+c 2-a 2=3bc,b 2-bc+c 2=a 2
根据余弦定理有a 2=b 2+c 2-2bccosA
∴b 2-bc+c 2=a 2=b 2+c 2-2bccosA
bc=2bccosAcosA=
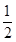 ∴A=60°又由sinA=2sinBcosC,
∴A=60°又由sinA=2sinBcosC,
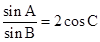 ,解得b=c,故三角形为.等边三角形,选D
,解得b=c,故三角形为.等边三角形,选D
【简答题】

[2/2000]在△ABC中,内角A,B,C所对的边分别为a,b,c,且acosB-bcosA= 【图片】c,当tan(A-B)取最大值时,角C的值为( )...
参考答案:
|
A
|
参考解析:
∵acosB-bcosA=
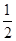 c
c
∴由正弦定理 =
=
 =
=
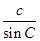
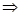 sinAcosB-sinBcosA=
sinAcosB-sinBcosA=
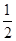 sinC,即sin(A-B)=
sinC,即sin(A-B)=
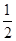 sinC
sinC
∵0〈sinC≤1
∴0<sin(A-B)≤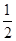 ,
,
在三角形ABC中,0〈A〈π,0〈B〈π
∴-π<A-B<π
∴0<A-B≤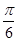 或
或
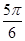 ≤A-B<π,
≤A-B<π,
又tanx在0<x≤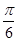 或
或
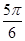 ≤x<π为增函数,且在0<x≤
≤x<π为增函数,且在0<x≤
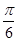 上的函数值为正,在
上的函数值为正,在
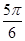 ≤x<π上的函数值为负,所以当A-B=
≤x<π上的函数值为负,所以当A-B=
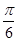 时,tan(A-B)有最大值.
时,tan(A-B)有最大值.
此时sin(A-B)=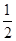 ,即sinC=1,解得C=
,即sinC=1,解得C=
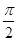 .
.
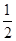 c
c
∴由正弦定理
 =
=
 =
=
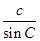
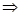 sinAcosB-sinBcosA=
sinAcosB-sinBcosA=
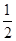 sinC,即sin(A-B)=
sinC,即sin(A-B)=
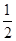 sinC
sinC
∵0〈sinC≤1
∴0<sin(A-B)≤
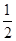 ,
,
在三角形ABC中,0〈A〈π,0〈B〈π
∴-π<A-B<π
∴0<A-B≤
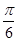 或
或
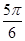 ≤A-B<π,
≤A-B<π,
又tanx在0<x≤
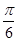 或
或
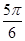 ≤x<π为增函数,且在0<x≤
≤x<π为增函数,且在0<x≤
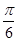 上的函数值为正,在
上的函数值为正,在
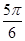 ≤x<π上的函数值为负,所以当A-B=
≤x<π上的函数值为负,所以当A-B=
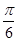 时,tan(A-B)有最大值.
时,tan(A-B)有最大值.
此时sin(A-B)=
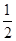 ,即sinC=1,解得C=
,即sinC=1,解得C=
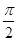 .
.
【简答题】

[3/2000]在△ABC中,角A,B,C的对边分别为a,b,c,且cosCcosB= 3a-cb.求:(1)sinB;(2)若b=42,且a=c,求边c长.
参考答案:
(1)∵△ABC中,
∴由正弦定理,得
即sinBcosC=3sinAcosC-cosBsinC, ∴sinBcosC+cosBsinC=3sinAcosC,即sin(B+C)=3sinAcosC, ∵△ABC中,B+C=π-A,得sin(B+C)=sinA ∴等式化简为sinA(1-3cosC)=0,结合sinA>0,得cosC=
因此,sinB=
(2)根据余弦定理b2=a2+c2-2accosB,得 32=a2+c2-2ac×
即边c长为2
|
参考解析:
cosCcosB
【简答题】

[4/2000]在△ABC中,角A,B,C所对应的边分别为a,b,c且c=3,a=2,a=2bsin A,则△ABC的面积为________.
参考答案:
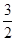
|
参考解析:
由题意知,bsin A=1,又由正弦定理得:bsin A=2sin B,故解得sin B=
 ,所以△ABC的面积为
,所以△ABC的面积为
 acsin B=
acsin B=
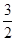 .
.
 ,所以△ABC的面积为
,所以△ABC的面积为
 acsin B=
acsin B=
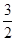 .
.
【简答题】

[5/2000]在 【图片】中,角 【图片】所对的边分别为 【图片】,且满足 【图片】, 【图片】. (I)求 【图片】的面积; (...
参考答案:
|
(1)2;(2)
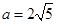 . .
|
参考解析:
本试题主要考查了解三角形的运用,第一问中运用,二倍角公式求解得到
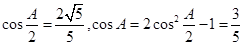 ,再由
,再由
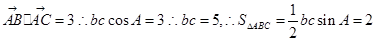
第二问,若b+c="6," bc=5,结合余弦定理可知a的值。
解: (1)因为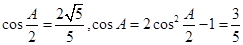 又由
又由
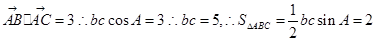
(2)对于bc=5,又b+c=6,b=5,c=1或b=1,c=5,由余弦定理得
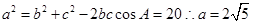
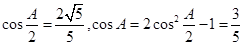 ,再由
,再由
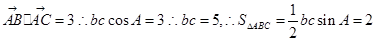
第二问,若b+c="6," bc=5,结合余弦定理可知a的值。
解: (1)因为
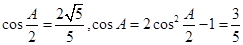 又由
又由
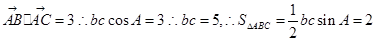
(2)对于bc=5,又b+c=6,b=5,c=1或b=1,c=5,由余弦定理得
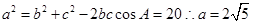
【简答题】

[6/2000]在△ABC中, 【图片】, 【图片】, 【图片】,则 【图片】等于 。
参考答案:
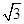
|
参考解析:
因为△ABC中,
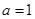 ,
,
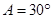 ,
,
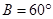 ,所以,由正弦定理得
,所以,由正弦定理得
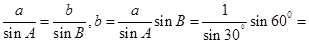
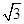 。
。
点评:简单题,已知两角及其一条对边,求其它边长,应用正弦定理。
【简答题】

[7/2000]在 【图片】中,若 【图片】,则该三角形的形状是 &n...
参考答案:
|
等腰或直角三角形
|
参考解析:
根据正弦定理可知
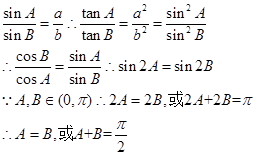
故三角形可能是等腰三角形也可能是直角三角形。故答案为等腰或直角三角形。
点评:解决该试题的关键是能根据表达式的特点,巧妙的结合正弦定理,将边化为角,然后结合三角函数的二倍角公式得到分析求解。
【简答题】

[8/2000]在△ABC中,AB= 【图片】,A=45°,C=75°,则BC= [ ] A.3- 【图片】B. 【图...
参考答案:
| A |
参考解析:
无
【简答题】

[9/2000]在△ABC中,A+C=2B,且最大角与最小角的对边长度之比为( 3+1):2.求A,B,C的大小.
参考答案:
| 因为在△ABC中,A+C=2B,所以180°=A+B+C=3B,于是B=60°.…(2分) 若最大角为A,则最小角为C.…(3分) 因为最大角与最小角的对边长度之比为(
由正弦定理得
所以cotC=1. …(12分) 因为C为三角形的内角,所以C=45°.…(13分) 因而A=75°.…(14分) 若最大角为C,最小角为A,则可得A=45°,从而C=75°.…(15分) 综上得A=75°,B=60°,C=45°或A=45°,B=60°,C=75°.…(16分) |
参考解析:
无
【简答题】

[10/2000](本小题满分12分) 如图,在△ABC中, 【图片】, 【图片】. (1) 求 【图片】; (2) 设 【图片】的中点为 【图片】,求中线 【图片】的...
参考答案:
|
解:(1)由
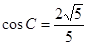 ,C是三解形内角, ,C是三解形内角,
得 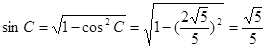 ………………2分 ………………2分
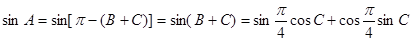
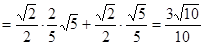 …………………6分 …………………6分
(2)在△ABC中,由正弦定理, 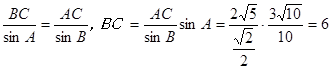
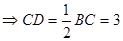 , …………………9分 , …………………9分
又在△ADC中, 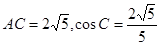 , ,
由余弦定理得, 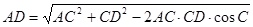
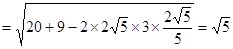 ……………12分 ……………12分
|
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





