创建自己的小题库
搜索
频率分布表、频率分布直方图、频率分布折线图、茎叶图题库
题数
1644
考试分类
高中数学>频率分布表、频率分布直方图、频率分布折线图、茎叶图
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-频率分布表、频率分布直方图、频率分布折线图、茎叶图
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/1644]在研究两个变量的关系时，可以通过残差 【图片】， 【图片】， ， 【图片】来判断模型拟合的效果，判断原始数据中是否存在可疑数据，这方面的分析工作称为 ...
参考答案：
|
残差
|
参考解析：
在研究两个变量的关系时，可以通过残差
，
， ，
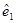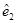来判断模型拟合的效果，判断原始数据中是否存在可疑数据，这方面的分析工作就是残差分析.
【简答题】
[2/1644]19C.解：由 【图片】得 【图片】，所以 【图片】，所以 【图片】，因为f(x)=x，所以 【图片】解得x=-1或-2或2，所以选C 调查某医院某段...
参考答案：
|
婴儿的出生时间与性别是相互独立的
|
参考解析：
解：由公式
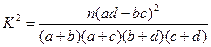
由于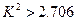
，所以只有10%的把握认为婴儿的出生时间与性别有关，故婴儿的出生时间与性别是相互独立的（也可以说没有充分的证据显示婴儿的性别与其出生时间有关。）
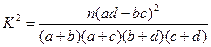
由于
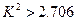，所以只有10%的把握认为婴儿的出生时间与性别有关，故婴儿的出生时间与性别是相互独立的（也可以说没有充分的证据显示婴儿的性别与其出生时间有关。）
【简答题】
[3/1644]一个样本容量为 【图片】的样本数据，它们组成一个公差不为 【图片】的等差数列 【图片】，若 【图片】，且 【图片】成等比数列，则此样本的中位数是___...
参考答案：
|
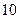
参考解析：
无
【简答题】
[4/1644]为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示： 【图片】（1）估...
参考答案：
|
(1)32 ；(2)
 .
|
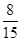参考解析：
(1)利用比例关系求第一问；(2)找出所有的基本事件，在所有的基本事件中找到符合题意的基本事件，再根据古典概型的概率计算公式求得相应事件的概率.
（1）由频率分布表可知：这15名乘客中候车时间少于10分钟的人数为8
所以，这60名乘客中候车时间少于10分钟的人数大约等于
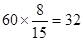人 4分
（2）设第三组的乘客为
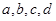，第四组的乘客为1，2
“抽到的两个人恰好来自不同的组”为事件
5分
所得基本事件共有15种，即：
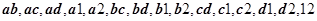8分
其中事件
包含基本事件
，共8种， 10分
由古典概型可得
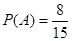12分.
【简答题】
[5/1644]某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的众数是85，乙班学生成绩的平均分为8...
参考答案：
|
D
|
参考解析：
甲班学生的众数是5，所以
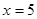，乙班学生的平均分是81，所以
，所以
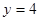，故：
.
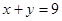【简答题】
[6/1644]对具有线性相关关系的变量x和y，由测得的一组数据已求得回归直线的斜率为6.5，且恒过(2,3)点，则这条回归直线的方程为________．
参考答案：
|
参考解析：
回归直线方程设为
,
,恒过点
代入
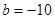,所以回归方程为
.
【简答题】
[7/1644]如图，是30名初三女学生1分钟内仰卧起坐次数的频数分布直方图（每组次数只含最小值而不含最大值），则仰卧起坐次数在25～45次的频率是 ______． ...
参考答案：
| 由频率分布直方图可知，“25～45”的学生人数有21人， ∴仰卧起坐次数在25～45次的频率=21÷30=0.7． 故答案为：0.7． |
参考解析：
无
【简答题】
[8/1644]某工厂对一批产品进行了抽样检测，下图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组...
参考答案：
| A |
参考解析：
无
【简答题】
[9/1644]为了检测某种产品的质量，抽取了一个容量为100的样本，数据的分组数如下：[10.75，10.85)，3；[10.85，10.95)，9；[10.95，...
参考答案：
解：(1)画出频率分布表： ；(2)频率分布直方图及频率分布折线图如下图所示，  ；(3)由上述图表可知数据落在[10.95，11.35）范围内的频率为0.87-0.12=0.75=75%， 即数据落在[10.95，11.35）范围内的可能性是75%； (4)数据小于11.20的可能性即数据小于11.20的频率，也就是数据在11.20处的累积频率，设为x， 则(x-0.41)÷(11.20-11.15)=(0.67-0.41)÷(11.25-11.15)， 所以x-0.41=0.13，即x=0.54， 从而估计数据小于11.20的可能性是54%。 |
参考解析：
无
【简答题】
[10/1644]某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60）…[90，100]后画出如下部分频率分布直...
参考答案：
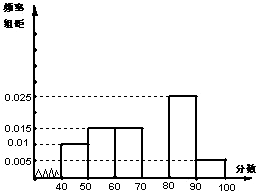 （Ⅰ）因为各组的频率和等于1，故第四组的频率：f4=1-（0.025+0.015*2+0.01+0.005）*10=0.3 （Ⅱ）依题意，60及以上的分数所在的第三、四、五、六组， 频率和为（0.015+0.03+0.025+0.005）*10=0.75所以，抽样学生成绩的合格率是75% 利用组中值估算抽样学生的平均分45•f1+55•f2+65•f3+75•f4+85•f5+95•f6 =45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71 估计这次考试的平均分是71． |
参考解析：
无
