
创建自己的小题库
搜索

抛物线的定义题库
题数
1630
考试分类
高中数学>抛物线的定义
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-抛物线的定义
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1630]已知动点P到定点(2,0)的距离比它到定直线l:x=-1的距离大1,则点P的轨迹方程为______.
参考答案:
| 由题意得,动点P到定点A(1,0)的距离和它到定直线x=-1的距离相等, 故P的轨迹是以点A为焦点,以直线x=-1为准线的抛物线,且p=2, 故抛物线方程为y2=4x, 故答案为:y2=4x. |
参考解析:
无
【简答题】

[2/1630]设抛物线y 2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( ) A.4B.6C.8D.12
参考答案:
|
B
|
参考解析:
∵点P到y轴的距离是4,延长使得和准线相交于点Q,则|PQ|等于点P到焦点的距离,而|PQ|=6,所以点P到该抛物线焦点的距离为6.
【方法技巧】求解抛物线上的点到焦点的距离和到准线的距离问题的技巧
抛物线上的点到焦点的距离与抛物线上的点到准线的距离经常相互转化:(1)若求点到焦点的距离,则可联想点到准线的距离;(2)若求点到准线的距离,则经常联想点到焦点的距离.解题时一定要注意.
【方法技巧】求解抛物线上的点到焦点的距离和到准线的距离问题的技巧
抛物线上的点到焦点的距离与抛物线上的点到准线的距离经常相互转化:(1)若求点到焦点的距离,则可联想点到准线的距离;(2)若求点到准线的距离,则经常联想点到焦点的距离.解题时一定要注意.
【简答题】

[3/1630]已知抛物线 【图片】的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 ...
参考答案:
|
2
|
参考解析:
略
【简答题】

[4/1630]若抛物线 【图片】的焦点是 【图片】,准线是 【图片】,则经过点 【图片】、 【图片】(4,4)且与 【图片】相切的圆共有 A. 【图片】个B. 【图...
参考答案:
|
C
|
参考解析:
分析:根据抛物线的方程求得焦点坐标和准线的方程,设出所求圆的圆心,表示出半径,则圆的方程可得,把M,F点的坐标代入整理求得h,和g,则圆的方程可得.
解:抛物线y 2=4x的焦参数p=2,所以F(1,0),直线l:x=-1,即x+1=0,
设经过点M(4,4)、F(1,0),且与直线l相切的圆的圆心为Q(g,h),
则半径为Q到,l的距离,即1+g,所以圆的方程为(x-g) 2+(y-h) 2=(1+g) 2,
将M、F的坐标代入,得(4-g) 2+(4-h) 2=(1+g) 2,(1-g) 2+(0-h) 2=(1+g) 2,
即h 2-8h+1=10g①,
h 2=4g②,②代入①,
得3h 2+16h-2=0,
解得h 1=
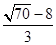 ,h
2=-
,h
2=-
 ,(经检验无增根)
,(经检验无增根)
代入②得g 1=
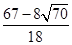 ,g
2=
,g
2=
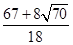 ,
,
所以满足条件的圆有两个:
(x-
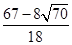 )
2+(y-
)
2+(y-
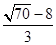 )
2=(
)
2=(
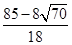 )
2,
)
2,
(x-
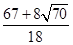 )
2+(y+
)
2+(y+
 )
2=(
)
2=(
 )
2.
)
2.
故选C
【简答题】

[5/1630]直线y=x+1被抛物线y 2=-2x所截得的弦的中点的坐标为____________.
参考答案:
|
(-2,-1)
|
参考解析:
由
 得x
2+4x+1=0.
得x
2+4x+1=0.
∴x 1+x 2=-4.
中点横坐标为-2,代入y=x+1,得y=-1.
 得x
2+4x+1=0.
得x
2+4x+1=0.
∴x 1+x 2=-4.
中点横坐标为-2,代入y=x+1,得y=-1.
【简答题】

[6/1630](本小题满分12分) 【图片】已知直线 【图片】过抛物线 【图片】的焦点 【图片】且与抛物线相交于两点 【图片】,自 【图片】向准线 【图片】 【图片...
参考答案:
|
(1) 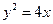
(2)略 (3) 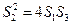
|
参考解析:
(Ⅰ)解:由条件知
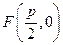 在直线
在直线
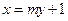 上,即
上,即
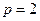 ,
,

所以抛物线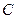 的方程为
的方程为
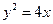 .………………2分
.………………2分
(Ⅱ) 由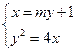 得
得
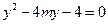 .………………3分
.………………3分
则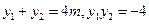 .………………4分
.………………4分
则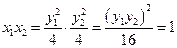 ,即有定值
,即有定值
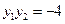 ,
,
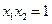 .………………6分
.………………6分
(III) 根据条件有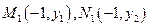 .
.
由抛物线的定义得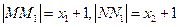 ,………………7分
,………………7分
于是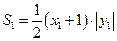 ,
,
 ,.
,.
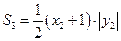 ……………8分
……………8分
 ………………9分
………………9分
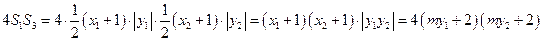
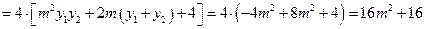 ,
,
则有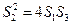 .………………12分
.………………12分
 在直线
在直线
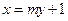 上,即
上,即
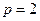 ,
,

所以抛物线
 的方程为
的方程为
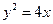 .………………2分
.………………2分
(Ⅱ) 由
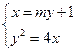 得
得
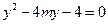 .………………3分
.………………3分
则
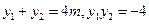 .………………4分
.………………4分
则
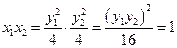 ,即有定值
,即有定值
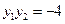 ,
,
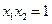 .………………6分
.………………6分
(III) 根据条件有
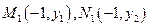 .
.
由抛物线的定义得
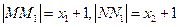 ,………………7分
,………………7分
于是
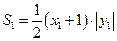 ,
,
 ,.
,.
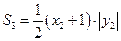 ……………8分
……………8分
 ………………9分
………………9分
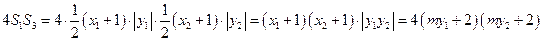
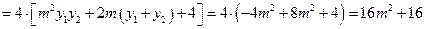 ,
,
则有
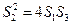 .………………12分
.………………12分
【简答题】

[7/1630]已知抛物线 【图片】的一个内接三角形的一顶点在原点,三条高线都通过抛物线的焦点,求这个三角形的外接圆的方程。
参考答案:

|
参考解析:
设
 为抛物线
为抛物线
 的内接三角形,因为垂心在焦点
的内接三角形,因为垂心在焦点
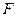 上,所以
上,所以
 ,即
,即
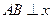 轴,垂足为
轴,垂足为
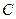 ,且由抛物线的对称性可知,
,且由抛物线的对称性可知,
 ,设
,设
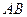 所在的直线方程为
所在的直线方程为
 ,所以
,所以
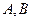 两点的坐标分别为
两点的坐标分别为
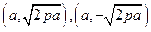 ,因为
,因为
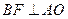 ,所以
,所以
 ,∴
,∴
 ,得
,得
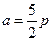 ,∵所求三角形外接圆过原点,故可设所求圆的方程为
,∵所求三角形外接圆过原点,故可设所求圆的方程为
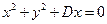 ,点
,点
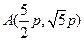 在圆上,代入A点的坐标,得
在圆上,代入A点的坐标,得
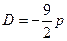 ,∴所求
,∴所求
 的外接圆的方程为
的外接圆的方程为
 。
。
 为抛物线
为抛物线
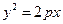 的内接三角形,因为垂心在焦点
的内接三角形,因为垂心在焦点
 上,所以
上,所以
 ,即
,即
 轴,垂足为
轴,垂足为
 ,且由抛物线的对称性可知,
,且由抛物线的对称性可知,
 ,设
,设
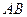 所在的直线方程为
所在的直线方程为
 ,所以
,所以
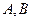 两点的坐标分别为
两点的坐标分别为
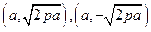 ,因为
,因为
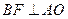 ,所以
,所以
 ,∴
,∴
 ,得
,得
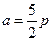 ,∵所求三角形外接圆过原点,故可设所求圆的方程为
,∵所求三角形外接圆过原点,故可设所求圆的方程为
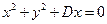 ,点
,点
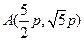 在圆上,代入A点的坐标,得
在圆上,代入A点的坐标,得
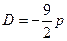 ,∴所求
,∴所求
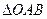 的外接圆的方程为
的外接圆的方程为
 。
。
【简答题】

[8/1630](14分)已知抛物线 【图片】的焦点F,直线l过点 【图片】。 (1)若点F到直线l的距离为 【图片】,求直线l的斜率; (2)设A,B为抛物线上两点...
参考答案:
|
(1)
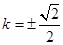 ;(2)见解析 ;(2)见解析
|
参考解析:
本试题主要是考查了抛物线的方程与性质的运用,以及点到直线的距离公式的求解,以及直线与抛物线位置关系的综合运用。
(1)设直线

(2)设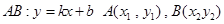
由 得
得
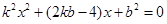 结合韦达定理得到AB的中点,然后利用斜率关系得到结果。
结合韦达定理得到AB的中点,然后利用斜率关系得到结果。
解:(1)设直线
 ……(4分)
……(4分)
(2)设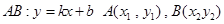
由 得
得
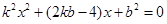
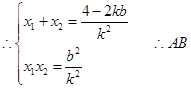 中点
中点
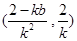
 ……(14分)
……(14分)
(1)设直线


(2)设
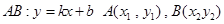
由
 得
得
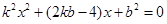 结合韦达定理得到AB的中点,然后利用斜率关系得到结果。
结合韦达定理得到AB的中点,然后利用斜率关系得到结果。
解:(1)设直线

 ……(4分)
……(4分)
(2)设
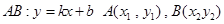
由
 得
得
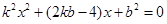
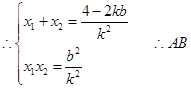 中点
中点
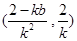
 ……(14分)
……(14分)
【简答题】

[9/1630]、抛物线 【图片】上有一点 【图片】到焦点的距离为5, (1)求 【图片】的值; (2)过焦点且斜率为1的直 【图片】线 【图片】交抛物线于 【图片】...
参考答案:
|
解:(1))抛物线的焦点是
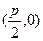 ,由题可得 ,由题可得
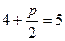 ,解得 ,解得
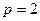
所以,抛物线的方程为  ,又点 ,又点
 在抛物线上,所以 在抛物线上,所以
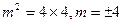
(2)设 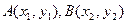 ,直线 ,直线
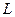 的方程为 的方程为
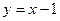
联立 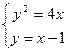 得 得
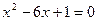
所以, 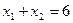 , ,
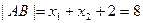 , ,
|
参考解析:
无
【简答题】

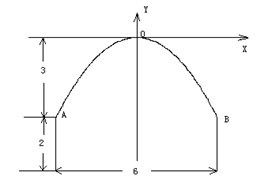
[10/1630]一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位: 【图片】),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3 【图片】,车与箱共...
参考答案:
|
车不能通过隧道.
|
参考解析:
如图,建立坐标系,则A(-3,-3),B(3, -3).
设抛物线方程为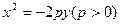 ,
,
将B点坐标代入,得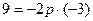 ,
,
∴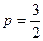 .∴抛物线方程为
.∴抛物线方程为
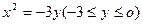 .
.
∵车与箱共高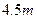 ∴集装箱上表面距抛物线型隧道拱顶
∴集装箱上表面距抛物线型隧道拱顶
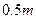 .
.
设抛物线上点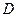 的坐标为
的坐标为
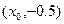 ,2则
,2则
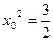 ,
,
∴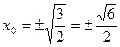 ,∴
,∴
 ,故此车不能通过隧道.
,故此车不能通过隧道.
设抛物线方程为
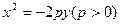 ,
,
将B点坐标代入,得
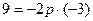 ,
,
∴
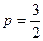 .∴抛物线方程为
.∴抛物线方程为
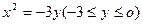 .
.
∵车与箱共高
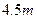 ∴集装箱上表面距抛物线型隧道拱顶
∴集装箱上表面距抛物线型隧道拱顶
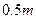 .
.
设抛物线上点
 的坐标为
的坐标为
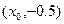 ,2则
,2则
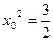 ,
,
∴
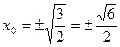 ,∴
,∴
 ,故此车不能通过隧道.
,故此车不能通过隧道.


 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





