
创建自己的小题库
搜索

函数图象题库
题数
1355
考试分类
高中数学>函数图象
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-函数图象
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1355]已知函数 【图片】, (1)在如图给定的直角坐标系内画出 【图片】的图象; 【图片】(2)写出 【图片】的单调递增区间.
参考答案:
|
(1)见解析;(2)
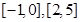 . .
|
参考解析:
(1)利用函数的解析式直接求出函数的图象,须注意各分段函数的定义域;(2)通过函数的图象直接写出函数的单调区间以及函数的值域.
(1)函数的图象如图所示:

(2)观察图象可知,
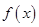 的单调递增区间为
的单调递增区间为
 .
.
【简答题】

[2/1355]函数 【图片】的定义域为开区间 【图片】,导函数 【图片】在 【图片】内的图象如图所示,则函数 【图片】在开区间 【图片】内有极小值点( ...
参考答案:
|
A
|
参考解析:
无
【简答题】

[3/1355]函数 【图片】由 【图片】确定,则方程 【图片】的实数解有( ) A.0个B.1个C.2个D.3个
参考答案:
|
D
|
参考解析:
由
 ,得
,得
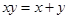 ,即
,即
 ,在直角坐标系中作出
,在直角坐标系中作出
 与
与
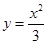 的图象,如图,由图可知方程的实数解有3个,故选D.
的图象,如图,由图可知方程的实数解有3个,故选D.

【简答题】

[4/1355]如图甲是某条公共汽车线路收支差额 【图片】与乘客量 【图片】的图象(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:...
参考答案:
|
B
|
参考解析:
直线的斜率说明票价问题;当x=0的点说明公司的成本情况,再结合图象进行说明.根据题意和图①知,两直线平行即票价不变,直线向上平移说明当乘客量为0时,收入是0但是支出的变少了,即说明了此建议是降低成本而保持票价不变;由图③看出,当乘客量为0时,支出不变,但是直线的倾斜角变大,即相同的乘客量时收入变大,即票价提高了,即说明了此建议是提高票价而保持成本不变,
【简答题】

[5/1355]在同一坐标系中画出函数 【图片】的图像,可能正确的是 【图片】
参考答案:
|
D
|
参考解析:
无
【简答题】

[6/1355]如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图...
参考答案:
| A |
参考解析:
无
【简答题】

[7/1355]函数y= 【图片】的图象关于x轴对称的图象大致是 [ ] A. 【图片】B. 【图片】C. 【图片】D...
参考答案:
| B |
参考解析:
无
【简答题】

[8/1355]已知函数 【图片】的图象与函数 【图片】的图象恰有两个交点,则实数 【图片】的取值范围是 .
参考答案:
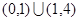 . .
|
参考解析:
因为原函数即为
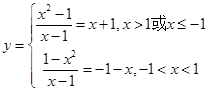 ,如图所示,又函数
,如图所示,又函数
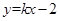 过定点
过定点
 ,当
,当
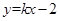 过
过
 与
与
 时,
时,
 ,而当
,而当
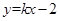 过
过
 与
与
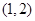 时,
时,
 ,又
,又
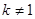 否则与
否则与
 平行不符合题意,结合图形可知当
平行不符合题意,结合图形可知当
 时,函数
时,函数
 的图象与函数
的图象与函数
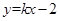 的图象恰有两个交点.
的图象恰有两个交点.
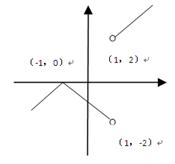
【简答题】

[9/1355]若 【图片】,则函数 【图片】的图像大致是( ) 【图片】
参考答案:
|
B
|
参考解析:
因为
 ,所以
,所以
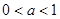 ,所以函数
,所以函数
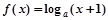 在其定义域上单调递减,又因为函数
在其定义域上单调递减,又因为函数
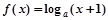 的定义域为
的定义域为
 ,所以选B
,所以选B
 ,所以
,所以
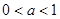 ,所以函数
,所以函数
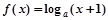 在其定义域上单调递减,又因为函数
在其定义域上单调递减,又因为函数
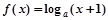 的定义域为
的定义域为
 ,所以选B
,所以选B
【简答题】

[10/1355]下列图象中不能作为函数图象的是( ) 【图片】
参考答案:
|
B
|
参考解析:
因为选项A中,能符合任意的一个x,对应唯一的y,因此是函数的图像;
选项B中,由于作一条垂直于x轴的直线,一个x能对应两个y,与定义相互矛盾,故不能作为函数图象。
选项C,D中,依次做一条直线垂直于x轴,都有唯一的一个y相对应,因此符合定义,成立。故选B。
点评:解决该试题的关键是理解函数中任意一个变量x,只能对应一个唯一的y,那么结合这个概念来判定符合题意的图像即可。

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





