创建自己的小题库
搜索
动能定理题库
题数
2000
考试分类
高中物理>动能定理
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中物理-动能定理
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
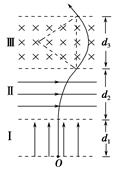
[1/2000]如图所示空间分为Ⅰ，Ⅱ，Ⅲ三个足够长的区域，各边界面相互平行，其中Ⅰ，Ⅱ区域存在匀强电场E I＝1.0×10 4 V/m，方向垂直边界面竖直向上；E ...
参考答案：
|
(1) v
1＝4×10
3 m/s (2) θ＝30° (3)6.12×10
-3s
|
参考解析：
(1)由动能定理得
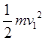＝qE
Id
1 ① （2分）
得：v 1＝4×10 3 m/s ② （1分）
(2)粒子在区域Ⅱ做类平抛运动．水平向右为y轴，竖直向上为x轴．设粒子进入区域Ⅲ时速度与边界的夹角为θ
tan θ＝
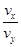③（1分）
v x＝v 1 v y＝at ④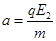（1分）
⑤（1分）
t＝
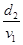⑥（1分）
把数值代入得θ＝30°⑦（1分）
(3)粒子进入磁场时的速度v 2＝2v 1 ⑧（1分）
粒子在磁场中运动的半径R＝
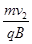＝10m ⑨（1分）
粒子在磁场中运动所对的圆心角为120° 因此
（1分）
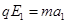
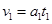（两式共1分）
由（2）得
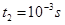
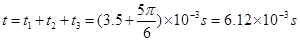（1+1=2分）
【简答题】
[2/2000]如图所示，在光滑水平面上放一木板B，B的左端放一木块A，A与B的接触面粗糙，在水平恒力F的作用下，可将A从B的左端拉到右端．第一次将B固定在水平面上，...
参考答案：
| 设B对A的滑动摩擦力为f，设木板B长度为L， 第一次拉A时由动能定理FL-fL=20J ① 设第二次拉A到B的右端时，B向前滑动的距离为s，对A由动能定理 （F-f） （L+s）=30J ② 对B由动能定理 fs=20J ③ 解①②③得F=15N L=4m 答：（1）水平恒力F的大小是15N （2）木板B的长度是4m． |
参考解析：
无
【简答题】
[3/2000]如图所示，半径为R的光滑半圆环轨道与高为8R的倾角为53°的粗糙斜面固定在同一竖直平面内，两轨道之间由一条光滑水平轨道CD相连，水平轨道与斜面间有一段...
参考答案：
（1）a球过圆轨道最高点A时 mg=m
a球从C运动到A，由机械能守恒定律
由以上两式求出 va=vC=
（2）b球从D运动到B，由动能定理得： -mg•8R-μmgcos53°
求出vb=2
（3）以a球、b球为研究对象，由动量守恒定律 mva=mbvb 求出mb=
弹簧的弹性势能 Ep=
求出 Eρ=7.5mgR 答： （1）a球释放时的速度大小是
（2）b球释放时的速度大小是2
（3）释放小球前弹簧的弹性势能是7.5mgR． |
参考解析：
无
【简答题】
[4/2000]如图所示，质量为m的小球从桌面竖直向上抛出，桌面离地高度为h1，小球能达到的最大高度离地为h．若以桌面为重力势能的零参考平面，不计空气阻力．以下说法中...
参考答案：
| 小球运动过程中，只受重力，机械能守恒，有 E=mg（h-h1）=
故选D． |
参考解析：
无
【简答题】
[5/2000]如图所示，距地面高为H处，以v 0的速度水平抛出一个小球，先后经过a、b两点后落地.若运动中空气阻力不计，小球通过a点时距地面高为h，小球质量为m，则...
参考答案：
|
B
|
参考解析：
由动能定理可知：
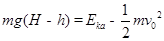，得在a点时的动能
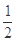m v
0
2+mg(H-h)。
故选：B。
点评：本题考查动能定理的应用，难度不大．
【简答题】
[6/2000]物体A放在水平面上与半径为r的圆柱体B用跨过定滑轮的细线相连接，半径为R的圆柱体C穿过细绳后搁在B上，三个物体的质量分别为mA=0.8kg，mB=mC...
参考答案：
| 设加速运动的末速度为v，由运动学公式得： 匀加速过程：v2=2a1H1 ① 匀减速过程：v2=2a2H2 ② 由①：②得：a1：a2=3：5 设A、B、C一起下降时绳中拉力为F1，C被固定挡板D截住，B继续下降时绳中拉力为F2 根据牛顿第二定律，有 匀加速过程： 对A：F1-μmAg=mAa1 ③ 对BC整体：（mB+mC）g-F1=（mB+mC）a1 ④ 由③④联立得：a1=
匀减速过程： 对A：μmAg-F2=mAa2 ⑥ 对B：F2-mBg=mBa2 ⑦ 联立⑥⑦得：a2=
联立⑤⑧两式，解得：μ=0.2 答：物体A与平面的动摩擦因数μ=0.2． |
参考解析：
(
mB+
mc)g-μ
mAg
mA+
mB+
mC
【简答题】
[7/2000]用相同材料做成的 A、 B两木块的质量之比为3∶2，初速度之比为2∶3，它们在同一粗糙水平面上同时开始沿直线滑行，直至停止，则它们（ &nb...
参考答案：
|
C
|
参考解析：
：加速度
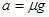与质量与初速度无关，A错误；根据公式
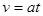，得时间之比为2：3，B错误；由公式
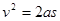得，
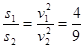，C正确、D错误。
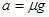与质量与初速度无关，A错误；根据公式
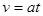，得时间之比为2：3，B错误；由公式
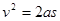得，
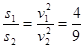，C正确、D错误。
【简答题】
[8/2000]质量为2kg的重物从30m高处由静止开始下落，下落过程中重物受到的空气阻力忽略不计。则重物下落2s时具有的动能为_____；重物下落高度为_____m...
参考答案：
|
400J 10
|
参考解析：
物体做自由落体运动，在2s内下落高度为
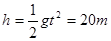，重力做功为mgh=100J，由动能定理可知动能为400J，设重力下落高度h时，动能为重力势能的一半，有
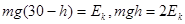，可得h=10m
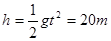，重力做功为mgh=100J，由动能定理可知动能为400J，设重力下落高度h时，动能为重力势能的一半，有
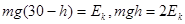，可得h=10m
【简答题】
[9/2000]物体沿直线运动的v－t关系如图所示，已知在第1秒内合外力对物体做的功为W，则 【图片】 [ ] A．从...
参考答案：
| CD |
参考解析：
无
【简答题】
[10/2000]如图所示，A、B为两块水平放置的金属板，通过闭合的开关S分别与电源两极相连，两极中央各有一个小孔a和b，在a孔正上方某处放一带电质点由静止开始下落，若...
参考答案：
| 设质点距离A板的高度h，A、B两板原来的距离为d，电压为U．质点的电量为q． A、由题质点到达b孔时速度恰为零，根据动能定理得mg（h+d）-qU=0． 若保持S闭合，将A板适当上移，设质点到达b时速度为v，由动能定理得mg（h+d）-qU=
B、若保持S闭合，将B板适当下移距离△d，由动能定理得mg（h+d+△d）-qU=
C、若断开S时，将A板适当上移，板间电场强度不变，设A板上移距离为△d，质点进入电场的深度为d′时速度为零． 由动能定理得mg（h-△d）-qEd′=0，又由原来情况有mg（h+d）-qEd=0．比较两式得，d′＜d，说明质点在到达b孔之前，速度减为零，然后返回．故C错误． D、若断开S，再将B板适当下移，根据动能定理可知，质点到达b孔原来的位置速度减为零，然后返回，不能到达b孔．故D错误． 故选B |
参考解析：
无
