
创建自己的小题库
搜索

排列与组合题库
题数
2000
考试分类
高中数学>排列与组合
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-排列与组合
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]小于50000且含有两个5而其他数字不重复的五位数有______个.
参考答案:
由题意,首位可以是1,2,3,4;两个5可以排在后4位中的任意两个位置,剩下两数,从其余8个数中选择,根据乘法原理,可得小于50000且含有两个5而其他数字不重复的五位数有
故答案为:1344. |
参考解析:
无
【简答题】

[2/2000]已知 【图片】,则x=" " .
参考答案:
|
略
|
参考解析:
无
【简答题】

[3/2000]设a1,a2,…,an是1,2,…,n的一个排列,把排在ai的左边且比ai小的数的个数称为ai的顺序数(i=1,2,…,n).如:在排列6,4,5,3...
参考答案:
| C |
参考解析:
无
【简答题】

[4/2000]A 2nn+3+A 4n+1=________.
参考答案:
|
744
|
参考解析:
由n+3≤2n,n+1≤4且n∈N
*,
∴n=3,A 2n n+3+A 4 n+1=6!+4!=744.
∴n=3,A 2n n+3+A 4 n+1=6!+4!=744.
【简答题】

[5/2000]将5名护士分配到某市的3家医院,每家医院至少分到一名护士的分配方案有( ) A.30种B.150种C.180种D.60种
参考答案:
|
B
|
参考解析:
解:由题意知本题是一个分步计数原理分两步完成:5名护士分配到某市的3家医院,每家医院至少分到一名护士可以分为5=1+1+3=1+2+2,这样可以得到
 ,选B
,选B
 ,选B
,选B
【简答题】

[6/2000]每天上午有4节课,下午有2节课,安排5门不同的课程,其中安排一门课两节连在一起上,则一天不同课表的种数为( ) A.96B.120C.480D.60...
参考答案:
| 先从5门课程中选1门连排的课程,有4种情况,即12,23,34,56; 将连排的课程看作1个整体,与其他4门课程,共5个元素全排列,有A55=120种情况, 则共有4×120=480种不同的安排方法; 故选C. |
参考解析:
无
【简答题】

[7/2000]某仪器显示屏上的每个指示灯泡均以红光或黄光或蓝光来表示不同的信号,已知一排有6个指示灯,每次显示其中的3个,且仅有2个相邻的,则一共可显示的不同信号数...
参考答案:
|
324
|
参考解析:
无
【简答题】

[8/2000]男教师6名,女教师4名,其中男女队长各1人,选派5人到灾区支教,队长中至少有一人参加,则不同的选派方法有( )种。 ...
参考答案:
|
D
|
参考解析:
分析:先求不考虑特殊情况的选派方法,再求出队长均未参加时选派方法,即可求得队长中至少有一人参加的不同的选派方法.
解:不考虑特殊情况,共有
 种选派方法,队长均未参加时,共有
种选派方法,队长均未参加时,共有
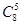 种选派方法
种选派方法
∴选派5人到灾区支教,队长中至少有一人参加,不同的选派方法有
 -
-
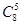 =196种
=196种
故选D.
【简答题】

[9/2000]已知 【图片】的展开式的第五项 【图片】的二项式系数与第三项的二项式系数的比是14:3,求展开式中不含 【图片】的项。
参考答案:
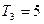 (10分) (10分)
|
参考解析:
无
【简答题】

[10/2000]书架上原来并排放着5本不同的书,现要再插入3本不同的书,那么不同的插法共有________种.
参考答案:
|
336
|
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





