
创建自己的小题库
搜索

解三角形题库
题数
2000
考试分类
高中数学>解三角形
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-解三角形
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000](本题满分12分)已知 【图片】、 【图片】、 【图片】分别是 【图片】的三个内角 【图片】、 【图片】、 【图片】所对的边; (1)若 【图片】面积...
参考答案:
|
(1)
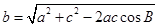 = =
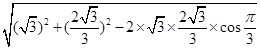 = =
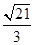 ; ;
(2) 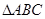 是等腰直角三角形。 是等腰直角三角形。
|
参考解析:
①利用△ABC面积为
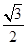 ,c和内角和定理直接求出B,通过余弦定理求出a的值.
,c和内角和定理直接求出B,通过余弦定理求出a的值.
②利用正弦定理化简关系式,求出角的关系即可判断△ABC的形状.
解:(1)
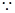
 、
、
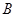 、
、
 成等差数列,
成等差数列,
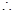
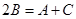 ,…………1分
,…………1分
又
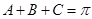
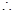
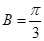 …………2分
…………2分
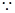

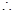
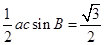 解得
解得
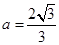 …………4分
…………4分
由余弦定理知,
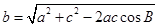
=
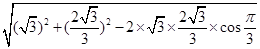 =
=
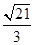 ………6分
………6分
(2)根据余弦定理,由
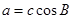 ,得
,得
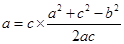 ,
,
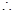
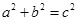 ,
,
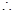
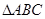 是直角三角形,
是直角三角形,
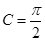 …………10分
…………10分
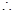
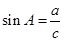 ,
,
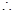
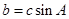 =
=
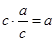 ,
,
故
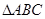 是等腰直角三角形。…………12分
是等腰直角三角形。…………12分
另法:根据正弦定理,由
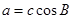 ,得
,得
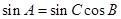 ,又
,又

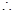
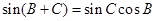
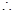
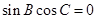
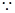
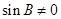 ,
,
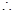
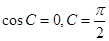 …………10分
…………10分
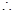
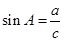 ,
,
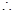
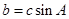 =
=
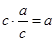 , 故
, 故
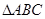 是等腰直角三角形。…………12分
是等腰直角三角形。…………12分
点评:解决该试题的关键是能将已知中等差数列得到角B的值,进而结合面积公式求解a,b的值。
【简答题】

[2/2000]在 【图片】中, 【图片】为锐角,角 【图片】所对应的边分别为 【图片】,且 【图片】, 【图片】。 (Ⅰ)求 【图片】的值; (Ⅱ)若 【图片】,求...
参考答案:
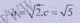
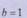
|
参考解析:
略
【简答题】

[3/2000]在△ABC中,角A,B,C所对的边分别为a,b,c,满足sin A2= 55,且△ABC的面积为2.(Ⅰ)求bc的值;(Ⅱ)若b+c=6,求a的值.
参考答案:
(Ⅰ)∵sin
∴cos
∴sinA=2sin
∵S△ABC=
∴bc=5. (Ⅱ)∵sin
∴cosA=1-2sin2
∵bc=5,b+c=6, ∴a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)=20 ∴a=2
|
参考解析:
A2
【简答题】

[4/2000]用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形(允许连接,但不允许折断),能够得到的三角形的最大面积为( ) A.8 cm2...
参考答案:
|
B
|
参考解析:
所求三角形的周长是肯定的,在周长一定的情况下,正三角形的面积最大.周长为20,那么最好每条边都是
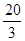 ,而那是不可能的,所以尽量往这种情况凑.因为只有5根,所以“6”肯定作为一条边,剩下2345,一看就知道2+5,和3+4分别为另两边时面积最大为6
,而那是不可能的,所以尽量往这种情况凑.因为只有5根,所以“6”肯定作为一条边,剩下2345,一看就知道2+5,和3+4分别为另两边时面积最大为6
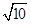 .
.
解:最大三角形的边长应为6,7,7,∴6边上的高为:2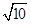 ,∴最大的三角形的面积为6
,∴最大的三角形的面积为6
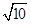 cm
2.
cm
2.
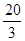 ,而那是不可能的,所以尽量往这种情况凑.因为只有5根,所以“6”肯定作为一条边,剩下2345,一看就知道2+5,和3+4分别为另两边时面积最大为6
,而那是不可能的,所以尽量往这种情况凑.因为只有5根,所以“6”肯定作为一条边,剩下2345,一看就知道2+5,和3+4分别为另两边时面积最大为6
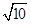 .
.
解:最大三角形的边长应为6,7,7,∴6边上的高为:2
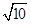 ,∴最大的三角形的面积为6
,∴最大的三角形的面积为6
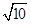 cm
2.
cm
2.
【简答题】

[5/2000]在△ 【图片】中,角A,B,C的对边分别为 【图片】,且 【图片】(1)求角B的大小; (2)若 【图片】且 【图片】,求 【图片】的取值范围.
参考答案:
|
(1)
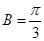
(2) 
|
参考解析:
解:(1) 在△
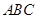 中,∵
中,∵
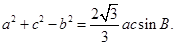 ,∴
,∴
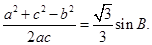 3分
3分
即:
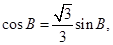 ∴
∴
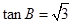 , 6分
, 6分
而
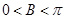 ,
,
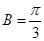 8分
8分
(2) ∵
 ∴
∴
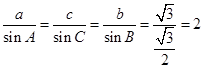 ,
,
∴
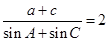 , 即:
, 即:
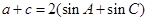 11分
11分
又∵
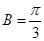 , ∴
, ∴
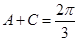 . 可设
. 可设
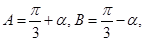
而
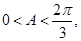 ∴
∴
 . ∴
. ∴
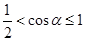
∴
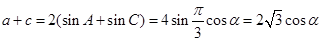
∴
 16分
16分
(注:第2问还可设问成求△
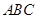 周长的最大值)
周长的最大值)
点评:主要是考查了解三角形的运用,属于基础题。
【简答题】

[6/2000]在△ABC中,若b=2asinB,则A等于( ) A.30°或60°B.45°或60°C.120°或60°D.30°或150°
参考答案:
|
D
|
参考解析:
由已知得sinB=2sinAsinB,
又∵A,B为△ABC的内角,
故sinB≠0,故sinA= ,
,
∴A=30°或150°.
又∵A,B为△ABC的内角,
故sinB≠0,故sinA=
 ,
,
∴A=30°或150°.
【简答题】

[7/2000]在△ABC中,若a、b、c分别为角A、B、C所对的边,且cos2B+cosB+cos(A-C)=1,则有( &nbs...
参考答案:
|
D
|
参考解析:
由
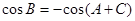 ,
,
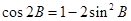 .所以cos2B+cosB+cos(A-C)=1可化为
.所以cos2B+cosB+cos(A-C)=1可化为
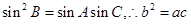 .所以
.所以
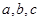 成等比数列.故选D.
成等比数列.故选D.
【简答题】

[8/2000](10分)(附加题)在锐角三角形 ABC中, a,b,c分别为角 A,B,C所对的边,且 B=3 A,求 【图片】的取值范围.
参考答案:
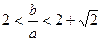
|
参考解析:
解:∵
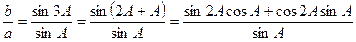
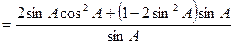
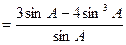
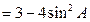
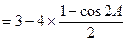
=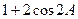
又∵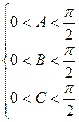 ∴
∴
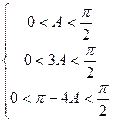
∴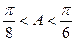 ∴
∴
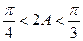
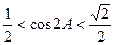
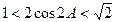
∴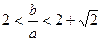
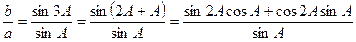
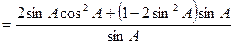
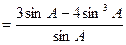
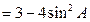
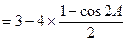
=
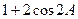
又∵
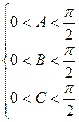 ∴
∴
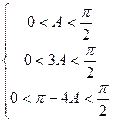
∴
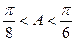 ∴
∴
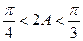
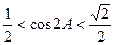
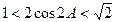
∴
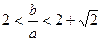
【简答题】

[9/2000]在△ABC中,若 【图片】,则角A=( ) A.30°B.60°C.120°D.150°
参考答案:
|
B
|
参考解析:
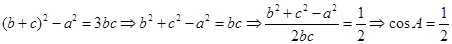 ,又因为角A是三角形的内角,所以
,又因为角A是三角形的内角,所以
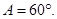
点评:正弦定理和余弦定理在解三角形中应用十分广泛,要准确选择,灵活应用.
【简答题】

[10/2000]在△ABC中,若a=50,b=25, A=45°则B= ...
参考答案:
|
60°或120°
|
参考解析:
由正弦定理得
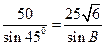 ,sinB=
,sinB=
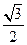 ,故B=60°或120°。
,故B=60°或120°。
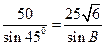 ,sinB=
,sinB=
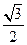 ,故B=60°或120°。
,故B=60°或120°。

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





