大学职业搜题刷题APP
下载APP
首页
课程
题库模板
Word题库模板
Excel题库模板
PDF题库模板
医考护考模板
答案在末尾模板
答案分章节末尾模板
题库创建教程
创建题库
登录
logo - 刷刷题
创建自己的小题库
搜索
充分条件与必要条件题库 - 刷刷题
充分条件与必要条件题库
题数
2000
考试分类
高中数学>充分条件与必要条件
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
微信内点击右上角“…”即可分享
去刷题
简介
高中数学-充分条件与必要条件
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/2000]“方程 【图片】+ 【图片】=1表示焦点在y轴上的椭圆”的充分不必要条件是 A． 【图片】B． 【图片】C． 【图片】D． 【图片】
参考答案：
A
参考解析：

方程 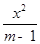+ 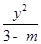=1表示焦点在y轴上的椭圆，则有
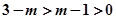
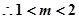，其充分不必要条件是
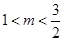
点评：椭圆焦点位置的确定是看标准方程中两分母的大小
【简答题】
[2/2000]指出下列各组命题中，p是q的什么条件？（1）p：（x-2）（x-3）=0；q：x-2=0。（2）p：四边形的对角线相等；q：四边形是平行四边形。（3）...
参考答案：
解：（1）∵（x-2）（x-3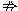）=0x-2=0，
（x-2）（x-3）=0x-2=0，
∴p是q的必要不充分条件。
（2）∵四边形的对角线相等四边形是平行四边形，四边形是平行四边形四边形的对角线相等，
∴p是q的既不充分也不必要条件。
（3）∵m＜-2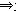方程x2-x-m=0无实根；
而方程x2-x-m=0无实根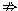m＜-2
∴p是q的充分不必要条件。
参考解析：
无
【简答题】
[3/2000]已知“x=1”是“x2=1”的（　　） A．充分不必要条件B．充要条件C．必要不充分条件D．既不充分又不必要条件
参考答案：
当x=1时，x2=1成立．
若x2=1，则x=1或x=-1．
∴“x=1”是“x2=1”的充分不必要条件，
故选：A．
参考解析：
无
【简答题】
[4/2000]函数f（x）=ax|x-b|在区间[0，+∞）上是增函数的充要条件是______．
参考答案：
f（x）=ax|x-b|=
ax 2-abx，x≥b
-ax 2+abx，x＜b
，由函数的解析式知，x=
b
2
两段上函数图象的对称轴，
当a＞0且b≤0时，函数在[b，+∞）是增函数，故在区间[0，+∞）上是增函数
当函数在区间[0，+∞）上是增函数时，必有a＞0，
b
2
≤0，即a＞0且b≤0
综上证明知，a＞0且b≤0是函数f（x）=ax|x-b|在区间[0，+∞）上是增函数的充要条件
故答案为：a＞0且b≤0
参考解析：
无
【简答题】
[5/2000]p：α=30°是q：sinα= 12成立的         ...
参考答案：
∵q：sinα=
1
2
，根据正弦函数图象的性质可知，
∴α=
π
6
+2kπ或α=
5
6
π +2kπ（k∈Z），
∴sinα=
1
2
推不出α=30°
又有α=30°?sinα=
1
2
，
∴p：α=30°是q：sinα=
1
2
成立的充分不必要条件，
故选B．
参考解析：
12
【简答题】
[6/2000]“a=1”是“函数f（x）=x+acosx在区间（0，π2）上为增函数”的______条件（在“充要”、“充分不必要”、“必要不充分”、“既不充分又不...
参考答案：
∵f（x）=x+acosx，
∴f'（x）=1-asinx，
若a=1时，f'（x）=1-sinx＞0，∴此时函数f（x）=x+acosx在区间（0，
π
2
）上为增函数．
当a=-1时，f'（x）=1+sinx＞0，满足在区间（0，
π
2
）上为增函数．
∴“a=1”是“函数f（x）=x+acosx在区间（0，
π
2
）上为增函数”的充分不必要条件．
故答案为：充分不必要．
参考解析：
无
【简答题】
[7/2000]已知 【图片】为两个命题，则“ 【图片】是真命题”是 “ 【图片】是真命题”的（ ）  A．充分不必要条件B．必要不充分条件C．充...
参考答案：
A
参考解析：

因为 是真命题，所以 是真命题；反之， 是真命题，则有多种情况：p,q均为真命题或p真q假或p假q真，即“ 是真命题”是 “ 是真命题”的充分不必要条件，故选A。
点评：基础题，解题时要牢记真值表，判断命题的真假是关键。
【简答题】
[8/2000]已知直线 【图片】： 【图片】和 【图片】： 【图片】 【图片】，则 【图片】的充要条件是 【图片】▲ ．
参考答案：
参考解析：
无
【简答题】
[9/2000]“等式sin（α+γ）=sin2β成立”是“α、β、γ成等差数列”的（　　） A．必要而不充分条件B．充分而不必要条件C．充分必要条件D．既不充分又不...
参考答案：
若等式sin（α+γ）=sin2β成立，
则α+γ=kπ+（-1）k•2β，
此时α、β、γ不一定成等差数列，
若α、β、γ成等差数列，
则2β=α+γ，
等式sin（α+γ）=sin2β成立，
所以“等式sin（α+γ）=sin2β成立”是“α、β、γ成等差数列”的．必要而不充分条件．
故选A．
参考解析：
无
【简答题】
[10/2000]“直线l垂直于△ABC的边AB，AC”是“直线l垂直于△ABC的边BC”的（　　） A．充要条件B．充分非必要条件C．必要非充分条件D．即非充分也非必...
参考答案：
设P：为“直线l垂直于△ABC的边AB，AC”，Q：为“直线l垂直于△ABC的边BC”．若P成立，则l⊥AB，l⊥AC，又∵AB∩AC=A，且AB、AC?面ABC，∴l⊥面ABC，又∵BC?面ABC∴l⊥BC，由P能推出Q．反之，若Q成立，由线面垂直的定义易知直线l不一定垂直于面ABC，所以直线l不一定垂直于△ABC的边AB，AC，故由Q推不出P．
故选B．
参考解析：
无
刷刷题-刷题-导入试题 - 刷刷题刷刷题-刷题-导入试题 - 刷刷题刷刷题-刷题-导入试题 - 刷刷题
刷刷题-刷题-导入试题 - 刷刷题
刷刷题-刷题-导入试题 - 刷刷题
刷刷题-单词鸭