
创建自己的小题库
搜索

余弦定理题库
题数
1700
考试分类
高中数学>余弦定理
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-余弦定理
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1700]已知 【图片】(Ⅰ)求函数f(x)的单调增区间.(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且a=1,b+c=2,f(A)= 【图片】,求...
参考答案:
解:(Ⅰ)因为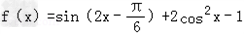 = 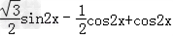 = 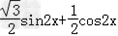 = =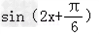 所以函数f(x)的单调递增区间是〔 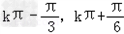 〕(k∈Z) 〕(k∈Z)(Ⅱ)因为f(x)=  ,所以 ,所以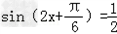 又0<A<π所以 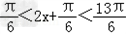 从而 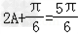 故A= 故A=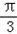 在△ABC中,∵a=1,b+c=2,A= 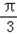 ∴1=b2+c2﹣2bccosA,即1=4﹣3bc. 故bc=1从而S△ABC= 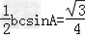 |
参考解析:
无
【简答题】

[2/1700]△ABC的内角A、B、C的对边长分别为a、b、c,若a2-c2=b,且b=3ccosA,则b=______.
参考答案:
| ∵b=3ccosA ∴b=3c×
将a2-c2=b代入上式得2b2=3b2-3b 解得b=3 故答案为:3 |
参考解析:
无
【简答题】

[3/1700]在△ABC中,若acosA-bcosB=0,则△ABC的形状一定是 [ ] A、等腰三角形B、直角三角...
参考答案:
| D |
参考解析:
无
【简答题】

[4/1700]已知△ABC的三边长都是有理数.(1)求证cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数.
参考答案:
(1)证明:设三边长分别为a,b,c,cosA=
∵a,b,c是有理数,b2+c2-a2是有理数,分母2bc为正有理数,又有理数集对于除法的具有封闭性, ∴
∴cosA是有理数. (2)①当n=1时,显然cosA是有理数; 当n=2时,∵cos2A=2cos2A-1,因为cosA是有理数,∴cos2A也是有理数; ②假设当n≤k(k≥2)时,结论成立,即coskA、cos(k-1)A均是有理数. 当n=k+1时,cos(k+1)A=coskAcosA-sinkAsinA,cos(k+1)A=coskAcosA-
解得:cos(k+1)A=2coskAcosA-cos(k-1)A ∵cosA,coskA,cos(k-1)A均是有理数,∴2coskAcosA-cos(k-1)A是有理数, ∴cosA,coskA,cos(k-1)A均是有理数. 即当n=k+1时,结论成立. 综上所述,对于任意正整数n,cosnA是有理数. |
参考解析:
b2+
c2-
a22bc
【简答题】

[5/1700]在△ABC中,若AB=1,BC=2,则∠C的取值范围是( )。
参考答案:
| 0°<C≤30° |
参考解析:
无
【简答题】

[6/1700]已知 【图片】外接圆 【图片】的半径为 【图片】,且 【图片】. 【图片】,从圆 【图片】内随机取一个点 【图片】,若点 【图片】取自 【图片】内的概...
参考答案:
|
B
|
参考解析:
由题意得
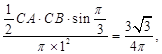 所以
所以
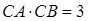 .在三角形AOB中,由于
.在三角形AOB中,由于
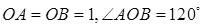 ,所以
,所以
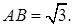 由余弦定理得
由余弦定理得
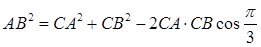 ,即
,即
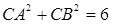 ,所以
,所以
 ,
,
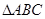 的形状为等边三角形.
的形状为等边三角形.
【简答题】

[7/1700]已知函数f(x)= 【图片】.(Ⅰ) 求函数f(x)的最小值和最小正周期;(Ⅱ)已知△ABC内角A,B,C的对边分别为a,b,c...
参考答案:
解:(Ⅰ)函数f(x)=  =  ﹣ ﹣  ﹣1 ﹣1=sin(2x﹣  )﹣1, )﹣1, ∴f(x)的最小值为﹣2,最小正周期为π. (Ⅱ)∵f(C)=sin(2C﹣  )﹣1=0,即 sin(2C﹣ )﹣1=0,即 sin(2C﹣ )=1, )=1,又∵0<C<π,﹣  <2C﹣ <2C﹣  < < , ,∴2C﹣  = = ,∴C= ,∴C=  . . ∵向量  与 与 共线, 共线,∴sinB﹣2sinA=0. 由正弦定理  ,得 b=2a,① ,得 b=2a,①∵c=3,由余弦定理得9=  ,② ,②解方程组①②,得 a=  b=2 b=2  . . |
参考解析:
无
【简答题】

[8/1700]在△ABC中,AB=3,BC=13,AC=4,则△ABC的面积是( ) A.3B.3 32C.33D.63
参考答案:
由余弦定理可知coaA=
所以sinA=
∴S△ABC=
故选C. |
参考解析:
AB2
+AC2
-BC22AB•AC
【简答题】

[9/1700]设△ ABC的内角 A、 B、 C所对的边分别为 a、 b、 c,已知 a=1, b=2,cos C=. (1)求△ ABC的周长; &nb...
参考答案:
|
(1)∵
c
2=
a
2+
b
2-2
abcos
C=1+4-4×=4,
∴ c=2,∴△ ABC的周长为 a+ b+ c=1+2+2=5. (2)∵cos C=,∴sin C===, ∴sin A===. ∵ a< c,∴ A< C,故 A为锐角, ∴cos A===. ∴cos( A- C)=cos Acos C+sin Asin C=×+×=. |
参考解析:
无
【简答题】

[10/1700]在△ABC中,若S△ABC= 14 3(b2+c2-a2),则角A=______.
参考答案:
在△ABC中,由余弦定理可得 b2+c2-a2=2bc•cosA,故由 S△ABC=
可得
故答案为 30°. |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





