创建自己的小题库
搜索
函数的零点与方程根的联系题库
题数
2000
考试分类
高中数学>函数的零点与方程根的联系
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-函数的零点与方程根的联系
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/2000]已知：θ∈[0，2π），sinθ、cosθ分别是方程x2-kx+x+1=0的两实根，求θ的值．
参考答案：
因为sinθ、cosθ分别是方程x2-kx+x+1=0的两实根，依题意：
因为（sinθ+cosθ）2=1+2sinθcosθ， 所以1+2（k+1）=k2，解得k=-1（k=3舍去）…6′ 所以
若sinθ=0，则cosθ=-1，所以θ=π； 若cosθ=0，则sinθ=-1，所以θ=
故θ的值为π或
|
参考解析：
| sinθ+cosθ=k |
| sinθcosθ=k+1 |
【简答题】
[2/2000]已知函数f（x）=3ax+1-3a，在区间（-1，1）内存在x0，使f（x0）=0，则a的取值范围是（ ） A．-1＜a＜ 16B．a＞ 16C．a...
参考答案：
令f （x）=3ax+1-3a=0得到 x=
所以根据题意有即-1＜
当a＞0时，解上述不等式得a＞
当a＜0时，解上述不等式得无解， 所以a的取值范围为a＞
故选B． |
参考解析：
无
【简答题】
[3/2000]下图是函数f（x）=x2+ax+b的部分图象，则函数g（x）=lnx+ f′（x）的零点所在的区间是 【图片】 [ ...
参考答案：
| C |
参考解析：
无
【简答题】
[4/2000]方程 【图片】的正实根个数为（ ） A．2个 B．3个C．4个D．无数个
参考答案：
|
B
|
参考解析：
在同一平面直角坐标系中分别作出函数
，
的图像，作图时，关注好
，故对
来说，只须作出
的图像即可
从而可得方程
的正实根个数为3个，选B.
【简答题】
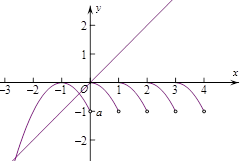
[5/2000]已知函数 【图片】,且函数 【图片】恰有3个不同的零点,则实数 【图片】的取值范围是（ ） ...
参考答案：
|
C
|
参考解析：
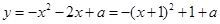，其顶点为
，点
在函数图象上，而点
不在函数图象上.结合图形可知，当
，函数
恰有3个不同的零点.
【简答题】
[6/2000]若一次函数f(x)＝ax＋b有一个零点2，那么函数g(x)＝bx 2－ax的零点是________．
参考答案：
|
0、－
|
参考解析：
由题意可得，b＝－2a且a≠0，由g(x)＝－2ax
2－ax＝0，得x＝0或x＝－
【简答题】
[7/2000]已知函数f（x）=x-2ax+1(a＞1，x∈R，x≠- 1a)；（1）试问：该函数的图象上是否存在不同的两点，它们的函数值相同，请说明理由；（2）若...
参考答案：
（1）令f（x1）=f（x2）
化简得：（2a+1）（x1-x2）=0 因为a＞1．所以等式成立的唯一条件是：x1=x2． ∴函数的图象上不存在不同的两点，它们的函数值相同 （2）F（x）=ax+f（x）=ax
a＞1，所以ax在区间（-∞，0]上为增函数，而f（x）在区间（-∞，0]上也是增函数． 根据函数单调性的性质：在同一单调区间内增函数+增函数，还是增函数． 可得函数F（x）=ax+f（x）在区间（-∞，0]上为增函数 又因为F（0）=-1 所以当x＜0时，f（x）＜-1 所以就不存在x＜0，使得f（x）=0． 即方程F（x）=0没有负根 （3）ax＞0， 如果b＜0，则：g（x）=（1-b）ax-b，为单调递增函数，无最小值． 如果b≥0，则： 当ax＞b时，g（x）=（1-b）ax-b， 当ax＜b时，g（x）=-（1+b）ax+b， 因为在两个开区间内，g（x）都是单调函数． 所以，要取得最小值的条件是，g（x）在（-∞，b]为减函数，在[b，+∞）为增函数． 所以： 1-b＞0 -（1+b）＜0 又∵b≥0 解得：0≤b＜1 |
参考解析：
x1-2a
x1+1
【简答题】
[8/2000]已知函数f（x）=ax2+（b+1）x+b-1，且a∈（0，3），则对于任意的b∈R，函数F（x）=f（x）-x总有两个不同的零点的概率是______...
参考答案：
| ∵F（x）=ax2+（b+1）x+b-1-x=ax2+bx+b-1， 函数F（x）总有两个不同的零点， 所以△=b2-4ab+4a＞0恒成立 令f（b）=b2-4ab+4a＞0 只需要△=16a2-16a＜0 ∴0＜a＜1． 所以，由几何概率的公式可得，所求的概率P=
故答案为
|
参考解析：
1-03-0
【简答题】
[9/2000]方程x-log2x=3有一实数解存在的区间是（ ） A．[0，2]B．[2，4]C．[4，8]D．[3，5]
参考答案：
| 构造函数f（x）=x-log2x-3，则 ∵f′(x)=1-
∴函数f（x）=x-log2x-3在[4，8]上单调增 又∵f（4）=4-2-3=-1＜0，f（8）=8-3-3=2＞0 ∴方程x-log2x=3有一实数解存在的区间是[4，8] 故选C． |
参考解析：
1xln2
【简答题】
[10/2000]函数f（x）=x3-2x2的图象与x轴的交点个数是（ ） A．3个B．2个C．1个D．0个
参考答案：
函数导数为f′(x)=3x2-4x=3x(x-
由f′(x)=3x(x-
由f′(x)=3x(x-
所以当x=0时，函数取得极大值f（0）=0． 当x=
所以函数f（x）=x3-2x2的图象与x轴的交点个数是2个． 故选B． |
参考解析：
无
