
创建自己的小题库
搜索

数列的概念及简单表示法题库
题数
1089
考试分类
高中数学>数列的概念及简单表示法
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-数列的概念及简单表示法
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1089]数列3,8,13,18,…的通项公式______.
参考答案:
| ∵数列数列3,8,13,18,…可写成3,3+5,3+2×5,3+3×5…, 这样,从第二项开始,每一项比前一项多5, ∴an=3+5(n-1)=5n-2, 故答案为:an=5n-2. |
参考解析:
无
【简答题】

[2/1089]数列{an}是递增数列,通项an=n2+kn,则实数k的取值范围是( ) A.(-3,+∞)B.[0,+∞)C.(-∞,-2]D.[-2,+∞)
参考答案:
| ∵数列{an}是递增数列 ∴an+1-an>0恒成立 即2n+1+k>0恒成立 即k>-2n-1恒成立 当n=1时,-2n-1最大为-3 ∴k>-3 故选A |
参考解析:
无
【简答题】

[3/1089]设数列 【图片】满足 【图片】, 【图片】(1)求 【图片】; (2)猜想出 【图片】的一个通项公式并用数学归纳法证明你的结论.
参考答案:
|
解:(1)
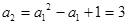
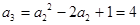 , ,
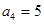 . .
(2) 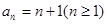 . .
下面用数学归纳法证明如下: ①当 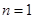 时, 时,
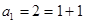 ,等式成立. ,等式成立.
②假设当 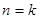 时等式成立,即 时等式成立,即
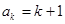 ,那么 ,那么
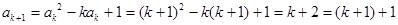 也就是说,当 也就是说,当
 时, 时,
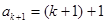 也成立. 根据(1)、(2)对于所有 也成立. 根据(1)、(2)对于所有
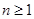 ,有 ,有
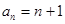 . .
|
参考解析:
本试题主要是考查了数列的递推关系的运用,以及根据数学归纳法加以证明猜想的结论的综合运用。分为两步骤,注意证明过程中必须要用到假设。
【简答题】

[4/1089] &n...
参考答案:
|
C
|
参考解析:
略
【简答题】

[5/1089]已知数列{an}的首项a1=1且满足 n≥2时,an=12an-1+12(n-1),则此数列的第三项是( ) A.1B.12C.34D.5...
参考答案:
因为a1=1,n≥2时,an=
所以a2=
a3=
故选C. |
参考解析:
12
【简答题】

[6/1089]右图给出一个数表,它有这样的规律:表中第一行只有一个数1,表中第 【图片】个数,且两端的数都是 【图片】,其余的每一个数都等于它肩上两个数的和,则第 ...
参考答案:
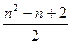
|
参考解析:
略
【简答题】

[7/1089]在数列{ 【图片】}中, 【图片】=2, 【图片】+1= 【图片】+Ln(1+ 【图片】),则 【图片】= A.2+LnnB.2+(n-1LnnC.2...
参考答案:
|
A
|
参考解析:
略
【简答题】

[8/1089]若数列 【图片】满足: 【图片】,则 【图片】_______.
参考答案:
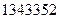
|
参考解析:
由
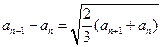 两边平方得
两边平方得
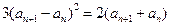 ,
,
又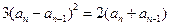 ,两式相减,得
,两式相减,得
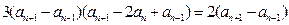 .
.
由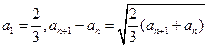 求得
求得
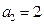 ,又由递推关系式易知数列
,又由递推关系式易知数列
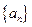 是单调递增数列,所以
是单调递增数列,所以
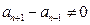 ,故
,故
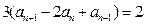 ,即
,即
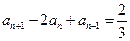 ,即
,即
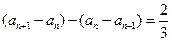 ,所以数列
,所以数列
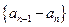 是以
是以
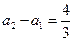 为首项,
为首项,
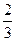 为公差的等差数列,所以
为公差的等差数列,所以
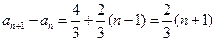 ,于是
,于是
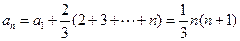 ,
,
所以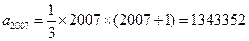 .
.
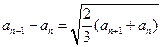 两边平方得
两边平方得
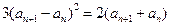 ,
,
又
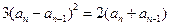 ,两式相减,得
,两式相减,得
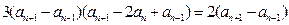 .
.
由
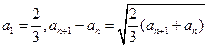 求得
求得
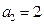 ,又由递推关系式易知数列
,又由递推关系式易知数列
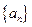 是单调递增数列,所以
是单调递增数列,所以
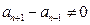 ,故
,故
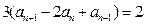 ,即
,即
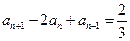 ,即
,即
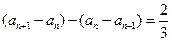 ,所以数列
,所以数列
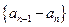 是以
是以
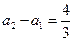 为首项,
为首项,
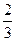 为公差的等差数列,所以
为公差的等差数列,所以
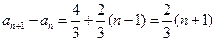 ,于是
,于是
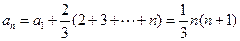 ,
,
所以
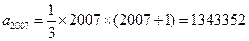 .
.
【简答题】

[9/1089]已知数列 【图片】满足 【图片】( 【图片】为常数, 【图片】),若 【图片】 【图片】,则 【图片】 ...
参考答案:
|
126
|
参考解析:
根据已知条件找到数列
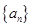 的特点,再去求解
的特点,再去求解
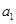 的值.
的值.
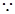
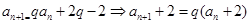 所以
所以
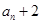 是以公比为q的等比数列.又因为
是以公比为q的等比数列.又因为
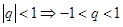 ,所以
,所以
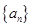 应是递减数列.又因为
应是递减数列.又因为
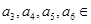
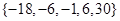 所以
所以
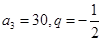 所以
所以
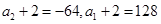 所以
所以
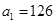
【简答题】

[10/1089]三个数成等差数列,其公差为d,如果最小数的2倍,最大数加7,则三个数成等比数列,且它们的积为1000,此时d为 A.8B.8或-15C.±8D.±15
参考答案:
|
B
|
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





