
创建自己的小题库
搜索

随机事件及其概率题库
题数
2000
考试分类
高中数学>随机事件及其概率
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-随机事件及其概率
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]下列说法:①必然事件的概率为1;②如果某种彩票的中奖概率为110,那么买1000张这种彩票一定能中奖;③某事件的概率为1.1;④互斥事件一定是对立事件...
参考答案:
| ①必然事件的概率为1;此说法是正确的; ②如果某种彩票的中奖概率为
③某事件的概率为1.1;概率的取值范围是[0,1],此说法是错误的; ④互斥事件一定是对立事件;由事件的定义知,对立事件一定是互斥事件,互斥事件不一定是对立事件,故此说法错误. 正确的说法仅有一个, 故选:B. |
参考解析:
110
【简答题】

[2/2000]一位国王的铸币大臣在每箱100枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测.方法一:在10箱中各任意抽查一枚;方法二:在5箱中各任...
参考答案:
方案一:此方案下,每箱中的劣币被选中的概率为
方案二:此方案下,每箱的劣币被选中的概率为
作差得P1-P2=(
∴P1<P2. 故选B |
参考解析:
1100
【简答题】

[3/2000]某商场举行购物抽奖促销活动,规定每位顾客从装有编号为0,1,2,3四个相同小球的抽奖箱中,每次取出一球记下编号后放回,连续取两次,若取出的两个小球号码...
参考答案:
| (1)设“中三等奖”为事件A,“中奖”为事件B, 从四个小球中有放回的取两个共有(0,0),(0,1),(0,2), (0,3),(1,0),(1,1)(1,2),(1,3),(2,0), (2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)16种不同的结果 两个小球号码相加之和等于4的取法有3种:(1,3),(2,2),(3,1) 两个小球号相加之和等于3的取法有4种:(0,3),(1,2),(2,1),(3,0) 由互斥事件的加法公式得:P(A)=
即中三等奖的概率为
(2)两个小球号码相加之和等于3的取法有4种;(0,3),(1,2),(2,1),(3,0) 两个小球相加之和等于4的取法有3种;(1,3),(2,2),(3,1) 两个小球号码相加之和等于5的取法有2种:(2,3),(3,2) 两个小球号码相加之和等于6的取法有1种:(3,3) 由互斥事件的加法公式得:P(B)=
即中奖的概率为:
|
参考解析:
无
【简答题】

[4/2000]盒子中有大小相同的3只白球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是( ) &...
参考答案:
|
A
|
参考解析:
分析:算出基本事件的总个数n=C 4 2=6,再 算出事件A中包含的基本事件的个数m=C 3 1=3,算出事件A的概率,即P(A)=
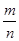 即可.
即可.
解:考查古典概型知识.
∵总个数n=C 4 2=6,
∵事件A中包含的基本事件的个数m=C 3 1=3
∴p=
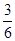 =
=

故填:A.
【简答题】

[5/2000]同时投掷两枚均匀的骰子,所得点数之和是8的概率是 ( ). A. 【图片】B. 【图片】C. 【图片】D. 【图...
参考答案:
|
C
|
参考解析:
列表如下:

从列表中可以看出,所有可能出现的结果共有36种,这些结果出现的可能性相等.∵点数的和为8的结果共有5种:(2,6),(3,,5),(4,4),(5,3),(6,2)∴点数的和为8的概率P=
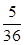 ,故选C.
,故选C.
【简答题】

[6/2000]一个袋中有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球,得到黑球的概率是25;从袋中任意摸出2个球,至少得到1个白球的概率是79.(Ⅰ)...
参考答案:
| (Ⅰ)记“从袋中任意摸出两个球,至少得到一个白球”为事件A, 设袋中白球的个数为x, 则P(A)=1-
得到x=5. 故白球有5个. 随机变量ξ的取值为0,1,2,3, ∴分布列是  ∴ξ的数学期望Eξ=
(Ⅱ)证明:设袋中有n个球,其中y个黑球,由题意得y=
∴2y<n,2y≤n-1, 故
记“从袋中任意摸出两个球,至少有1个黑球”为事件B, 则P(B)=
∴白球的个数比黑球多,白球个数多于
故袋中红球个数最少. |
参考解析:
| C | 210-x |
| C | 210 |
【简答题】

[7/2000]从分别写有0,1,2,3,4的五张卡片中取出一张卡片,记下数字后放回,再从中取出一张卡片.则两次取出的卡片上的数字之和恰好等于4的概率是_______...
参考答案:
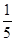
|
参考解析:
从0,1,2,3,4五张卡片中取出两张卡片的结果有25种,数字之和恰好等于4的结果有(0,4),(1,3),(2,2),(3,1),(4,0),所以数字和恰好等于4的概率是P=
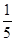 .
.
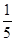 .
.
【简答题】

[8/2000]在一次数学测验后,班级学委对选答题的选题情况进行了统计,如下表: 几何证明选讲坐标系与参数方程不等式选讲合计男同学(人数)124622女同...
参考答案:
|
(1)有95%的把握认为选做“几何类”或“代数类”与性别有关(2)①
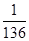 ② ②
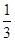
|
参考解析:
(1)由表中数据得K
2的观测值k=
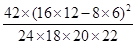 =
=
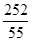 ≈4.582>3.841.
≈4.582>3.841.
所以,据此统计有95%的把握认为选做“几何类”或“代数类”与性别有关.
(2)由题可知在“不等式选讲”的18位同学中,要选取3位同学.
①方法一:令事件A为“这名班级学委被抽到”;事件B为“两名数学科代表被抽到”,则P(A∩B)=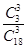 ,P(A)=
,P(A)=
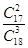
所以P(B|A)= =
=
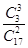 =
=
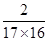 =
=
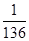 .
.
方法二:令事件C为“在这名学委被抽到的条件下,两名数学科代表也被抽到”,则P(C)=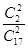 =
=
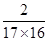 =
=
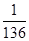 .
.
②由题知X的可能值为0,1,2.
依题P(X=0)=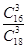 =
=
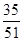 ;P(X=1)=
;P(X=1)=
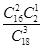 =
=
 ;P(X=2)=
;P(X=2)=
 =
=
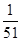 .从而X的分布列为
.从而X的分布列为
于是E(X)=0×
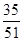 +1×
+1×
 +2×
+2×
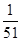 =
=
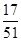 =
=
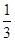 .
.
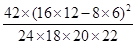 =
=
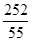 ≈4.582>3.841.
≈4.582>3.841.
所以,据此统计有95%的把握认为选做“几何类”或“代数类”与性别有关.
(2)由题可知在“不等式选讲”的18位同学中,要选取3位同学.
①方法一:令事件A为“这名班级学委被抽到”;事件B为“两名数学科代表被抽到”,则P(A∩B)=
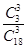 ,P(A)=
,P(A)=
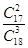
所以P(B|A)=
 =
=
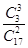 =
=
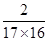 =
=
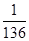 .
.
方法二:令事件C为“在这名学委被抽到的条件下,两名数学科代表也被抽到”,则P(C)=
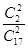 =
=
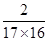 =
=
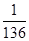 .
.
②由题知X的可能值为0,1,2.
依题P(X=0)=
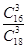 =
=
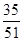 ;P(X=1)=
;P(X=1)=
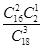 =
=
 ;P(X=2)=
;P(X=2)=
 =
=
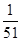 .从而X的分布列为
.从而X的分布列为
| X |
0 |
1 |
2 |
| P |
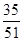 |
 |
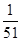 |
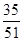 +1×
+1×
 +2×
+2×
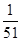 =
=
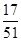 =
=
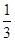 .
.
【简答题】

[9/2000]袋子中原有若干个黑球,现放入lO个白球,所有的球只有颜色不同,从袋子中随机取球,每次1个,取后放回.若在100次取球中有20次是白球,则估计袋子中原有...
参考答案:
由于每次取出的球为白球的概率都是相等的,若在100次取球中有20次是白球,则白球的数量约占总数的
设黑球有x个,则由
故答案为40. |
参考解析:
无
【简答题】

[10/2000]中国象棋红方棋子按兵种不同分布如下:1个帅,5个兵,“士、象、马、车、炮”各2个,将所有棋子反面朝上放在棋盘中,任取一个不是兵和帅的概率是( ) A...
参考答案:
| 所有机会均等的可能共有16种. 而不是兵和帅的机会有10种, 因此任取一个不是兵和帅的概率是:
故选D. |
参考解析:
1016

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





