
创建自己的小题库
搜索

简单的逻辑联结词题库
题数
1252
考试分类
高中数学>简单的逻辑联结词
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-简单的逻辑联结词
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1252]命题“ 【图片】, 【图片】”的否定是 &...
参考答案:
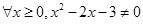
|
参考解析:
命题“
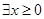 ,
,
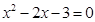 ”是一个特称命题,其否定是一个全称命题,即命题“
”是一个特称命题,其否定是一个全称命题,即命题“
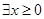 ,
,
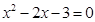 ”的否定是:
”的否定是:
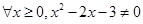 。
。
点评:注意命题的否定和否命题的区别。
【简答题】

[2/1252]命题“ 【图片】x∈R, 【图片】”的否定是 &nbs...
参考答案:
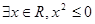
|
参考解析:
全称命题的否定是特称命题,需将全称量词改为特称量词,并否定满足的条件,
 的否定是
的否定是
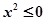
点评:全称命题
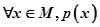 的否定是特称命题
的否定是特称命题
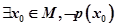
【简答题】

[3/1252](12分)已知命题p:∀x∈[1,2],x 2-a≥0.命题q:∃x 0∈R,使得x+(a-1)x 0+1<0.若“p或q”为真,“p且q”为假...
参考答案:
|
解:由条件知,a≤x
2对∀x
 ∈[1,2]成立,∴a≤1; ∈[1,2]成立,∴a≤1;
∵∃x 0∈R,使x+(a-1)x 0+1<0成立, ∴不等式x 2+(a-1)x+1<0有解,∴Δ=(a-1) 2-4>0,∴a>3或a<-1; ∵p或q为真,p且q为假, ∴p与q一真一假. ①p真q假时,-1≤a≤1; ②p假q真时,a>3. ∴实数a的取值范围是a>3或-1≤a≤1. |
参考解析:
略
【简答题】

[4/1252]命题“ 【图片】”的否定是: ;
参考答案:

|
参考解析:
特称命题的否定为全称命题。
【简答题】

[5/1252]① 【图片】;② 【图片】; ③ 【图片】抛物线 【图片】过原点;④ 【图片】其中满足p是q的充要条件的命题个数为 A.0B.1 C.2D.3
参考答案:
|
C
|
参考解析:
①
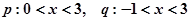 ,p是q的充分不必要条件;②
,p是q的充分不必要条件;②
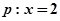 或
或
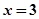
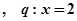 ,p是q必要不充分条件;③
,p是q必要不充分条件;③
 抛物线
抛物线
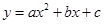 过原点,p是q的充要条件;④
过原点,p是q的充要条件;④
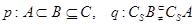 ,p是q的充要条件
,p是q的充要条件
点评:若
 则
则
 是
是
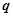 的充分条件,
的充分条件,
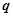 是
是
 的必要条件
的必要条件
【简答题】

[6/1252]已知下列三个命题: (1) 【图片】(2) 【图片】(3) 【图片】选择其中两个作为题设,一个作为结论,写出一个逆否命 题是真命题的命题_____.
参考答案:
|
若
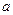 是正数,且 是正数,且
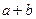 是负数,则 是负数,则
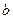 是负数 是负数
|
参考解析:
无
【简答题】

[7/1252]下列命题中,所有正确命题的个数为( ) ①命题“若 【图片】”的逆命题是真命题; ② 【图片】③若随机变量 【图片】...
参考答案:
|
C
|
参考解析:
无
【简答题】

[8/1252]给出下列四个命题,其中正确的是( ) A.在空间若两条直线不相交,则它们一定平行B.直线a不平行于平面 【图片】,则...
参考答案:
|
D
|
参考解析:
分析:根据由不重合的两直线之间的关系,直线与平面间的关系,线面角的知识逐一排除。
解答:
选项A:在空间若两条直线不相交,两直线可以异面,所以排除;
选项B:a可以在面α内,这样α内可以有与a平行的直线,所以排除;
选项C:两面相交,a可以与两个面平行,及夹角为00,所以两面可以不平行,所以排除;
故选D。
点评:本题考查直线之间的关系,直线与平面间的关系,线面角.重点在于知识的应用,方法是举反例。
【简答题】

[9/1252]在△ABC中“ 【图片】”是“△ABC为直角三角形”的( ). A.充分不必要条件B.必要不充分条件 C.充要条件...
参考答案:
|
A
|
参考解析:
根据题意,由于
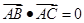 ∴-ac•cosα=0,即cosα=0,∵α∈(0,π)∴α=
∴-ac•cosα=0,即cosα=0,∵α∈(0,π)∴α=
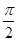 ,则△ABC为直角三角形;而当△ABC为直角三角形时,B不一定为直角,则
,则△ABC为直角三角形;而当△ABC为直角三角形时,B不一定为直角,则
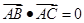 不一定成立,因此可知条件是结论成立的充分不必要条件,选A
不一定成立,因此可知条件是结论成立的充分不必要条件,选A
点评:此题考查了充分,必要及充要条件的判断,三角形形状的判断,涉及的知识有:平面向量的数量积运算法则,余弦函数的奇偶性,以及特殊角的三角函数值,熟练掌握法则及余弦函数的奇偶性是解本题的关键
【简答题】

[10/1252]设p、q是两上命题, 【图片】( ) A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
参考答案:
|
A
|
参考解析:
因为
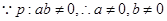 ,同时
,同时
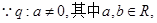 则根据集合的大小关系可知,前者表示的集合小,后者表示的集合大,
则根据集合的大小关系可知,前者表示的集合小,后者表示的集合大,
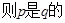 充分不必要条件,故选A.
充分不必要条件,故选A.
点评:解决该试题的关键是对于命题P,Q的理解和准确的表示,进而结合集合的思想,大集合是小集合成立的必要不充分条件,小集合是大集合的充分不必要条件。

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





