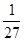离散型随机变量的期望与方差题库 - 考试题库

【简答题】

[1/1027]在一个圆锥体的培养房内培养了40只蜜蜂，准备进行某种实验，过圆锥高的中点有一个不计厚度且平行于圆锥底面的平面把培养房分成两个实验区，其中小锥体叫第一实...

参考答案：

解：
（1）由题意知蜜蜂落入培养房内任何位置是等可能的，且蜜蜂落入哪个位置相互之间是不受影响的，可以得到这是一个等可能事件的概率，记“蜜蜂落入第一实验区”为事件A，“蜜蜂落入第二实验区”为事件B．依题意，

∴

∴蜜蜂落入第二实验区的概率为

．
（2）本题符合独立重复试验，记“恰有一只红色蜜蜂落入第二实验区”为事件C，则

∴恰有一只红色蜜蜂落入第二实验区的概率

．
（3）因为蜜蜂落入培养房内任何位置是等可能的，且蜜蜂落入哪个位置相互之间是不受影响的，∴变量X满足二项分布，即X～

∴随机变量X的数学期望EX=40×

=5

参考解析：

无

【简答题】

[2/1027]【图片】【图片】（1）求乙运动员击中8环的概率，并求甲、乙同时击中9环以上（包括9环）的概率。（2） ...

参考答案：

（1）0.3575 （2）8.8

参考解析：

无

【简答题】

[3/1027]一离散型随机变量【图片】的概率分布列如下，且【图片】则【图片】 ...

参考答案：

0

参考解析：

由题意知

所以a=b=0.4,所以b-a=0

【简答题】

[4/1027]今年雷锋日，某中学从高中三个年级选派4名教师和20名学生去当雷锋志愿者，学生的名额分配如下：高一年级高二年级高三年级10人6人4人（I）若从20名学生...

参考答案：

（I）设“他们中恰好有1人是高一年级学生”为事件A，则P(A)=

C

110

C

210

C

320

=

15

38

答：若从选派的学生中任选3人进行文明交通宣传活动，他们中恰好有1人是高一年级学生的概率为

15

38

．…（4分）
（II）解法1：ξ的所有取值为0，1，2，3，4．由题意可知，每位教师选择高一年级的概率均为

1

3

．所以…（6分）P(ξ=0)=

C

04

(

1

3

)0(

2

3

)4=

16

81

；P(ξ=1)=

C

14

(

1

3

)1(

2

3

)3=

32

81

；P(ξ=2)=

C

24

(

1

3

)2(

2

3

)2=

24

81

=

8

27

；P(ξ=3)=

C

34

(

1

3

)3(

2

3

)1=

8

81

；
P(ξ=4)=

C

44

(

1

3

)4(

2

3

)0=

1

81

．…（11分）
随机变量ξ的分布列为：

ξ

0

1

2

3

4

P

16

81

32

81

8

27

8

81

1

81

…（12分）
所以Eξ=0×

16

81

+1×

32

81

+2×

24

81

+3×

8

81

+4×

1

81

=

4

3

…（13分）
解法2：由题意可知，每位教师选择高一年级的概率均为

1

3

．…（5分）
则随机变量ξ服从参数为4，

1

3

的二项分布，即ξ～B(4，

1

3

)．…（7分）
随机变量ξ的分布列为：

ξ

0

1

2

3

4

P

16

81

32

81

8

27

8

81

1

81

所以Eξ=np=4×

1

3

=

4

3

…（13分）

参考解析：

C

110

C

210

C

320

【简答题】

[5/1027]某市职教中心组织厨师技能大赛，大赛依次设基本功（初赛）、面点制作（复赛）、热菜烹制（决赛）三个轮次的比赛，已知某选手通过初赛、复赛、决赛的概率分别是3...

参考答案：

（I）ξ可能取值为1，2，3．-------------------------------（2分）
记“该选手通过初赛”为事件A，“该选手通过复赛”为事件B，则
P（ξ=1）=P（

.

A

）=1-

3

4

=

1

4

；P（ξ=2）=P（A

.

B

）=P（A）P（

.

B

）=

3

4

×(1-

2

3

) =

1

4

；
P（ξ=3）=P（AB）=P（A）P（B）=

3

4

×

2

3

=

1

2

--------------------（5分）
ξ的分布列为：

ξ

1

2

3

P

1

4

1

4

1

2

ξ的数学期望Eξ=1×

1

4

+2×

1

4

+3×

1

2

=

9

4

------------------------（7分）
（Ⅱ）当ξ=1时，f（x）=3sin（

π

2

x+

π

2

）=3cos

π

2

x ，∴f（x）为偶函数；
当ξ=2时，f（x）=3sin（

π

2

x+π ）=-3sin

π

2

x ，∴f（x）为奇函数；
当ξ=3时，f（x）=3sin（

π

2

x+

3π

2

），∴f（x）为偶函数；
∴事件D发生的概率是

2

3

．-----------------------------------（12分）

参考解析：

.A

【简答题】

[6/1027]一个口袋中装有大小相同的2个白球和4个黑球，要从中摸出两个球．（Ⅰ）采取放回抽取方式，求摸出两球颜色恰好不同的概率；（Ⅱ）采取不放回抽取方式，记摸得白...

参考答案：

（Ⅰ）解法一：“有放回摸两次，颜色不同”指“先白再黑”或“先黑再白”，
记“有放回摸球两次，两球恰好颜色不同”为事件A，…（2分）
∵“两球恰好颜色不同”共2×4+4×2=16种可能，…（4分）
∴P(A)=

16

6×6

=

4

9

．…（6分）
解法二：“有放回摸取”可看作独立重复实验，…（2分）
∵每次摸出一球得白球的概率为P=

2

6

=

1

3

．…（4分）
∴“有放回摸两次，颜色不同”的概率为P2(1)=

C

12

•p•(1-p)=

4

9

．…（6分）
（Ⅱ）设摸得白球的个数为ξ，依题意得：
∵P(ξ=0)=

4

6

×

3

5

=

2

5

，P(ξ=1)=

4

6

×

2

5

+

2

6

×

4

5

=

8

15

，P(ξ=2)=

2

6

×

1

5

=

1

15

．…（9分）
∴它的分布列为

ξ

0

1

2

P

2

5

8

15

1

15

∴Eξ=0×

1

2

+1×

8

15

+2×

1

15

=

2

3

，…（12分）Dξ=(0-

2

3

)2×

2

5

+(1-

2

3

)2×

8

15

+(2-

2

3

)2×

1

15

=

16

45

．…（14分）

参考解析：

166×6

【简答题】

[7/1027]某市公租房房屋位于A、B、C三个地区，设每位申请人只申请其中一个片区的房屋，且申请其中任一个片区的房屋是等可能的，求该市的任4位申请人中： (1)若有...

参考答案：

（1）

（2）X的分布列为：

X	1	2	3
p

参考解析：

X
1
2
3
p

【简答题】

[8/1027]若离散型随机变量【图片】的分布列如下：【图片】 0&...

参考答案：

C

参考解析：

根据题意，利用b+0.4=1,b=0.6,根据题意可知，x的期望值为0.4，
方差为0.5[（0-0.4）

+(1-0.4)

]=0.24,故可知答案为C.
点评：主要是考查了随机变量的分布列的期望和方差的运用，属于基础题。

【简答题】

[9/1027]袋中装有10个大小相同的小球，其中黑球3个，白球n个（4≤n≤6），其余均为红球。（1）从袋中一次任取2个球，如果这2个球颜色相同的概率是【图片】...

参考答案：

解：（1）红球3个；
（2）①ξ的可能取值为2，3，4，6，
P（ξ=2）=

，P（ξ=3）=

，P（ξ=4）=

，P（ξ=5）=

，P（ξ=6）=

，
∴ξ的分布列为

ξ	2	3	4	5	6
P

∴Eξ=2×

+3×

+4×

+5×

+6×

=

。
②

。

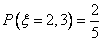参考解析：

ξ

2

3

4

5

6

P

【简答题】

[10/1027]（本小题满分12分）某校举行环保知识大奖赛，比赛分初赛和决赛两部分，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对...

参考答案：

（1）

（2）

（3）

参考解析：

解：（1）设甲选手答对一个问题的正确率为

，则

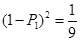
故甲选手答对一个问题的正确率

3分
（Ⅱ）选手甲答了3道题目进入决赛的概率为

=

4分
选手甲答了4道题目进入决赛的概率为

5分
选手甲答了5道题目进入决赛的概率为

6分
选手甲可以进入决赛的概率

7分
（Ⅲ）

可取3，4，5则有

8分

9分

10分

	3	4	5

故

12分
点评：解决该试题的关键是能理解独立事件的概念分情况来求解概率值，同时能结合独立重复试验的概率公式求解分布列和期望值。属于基础题。