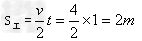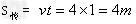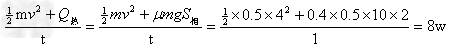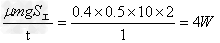创建自己的小题库
搜索

能量转化与守恒定律题库
题数
193
考试分类
高中物理>能量转化与守恒定律
售价
¥15
 手机预览
手机预览
收藏
分享
去刷题
简介
高中物理-能量转化与守恒定律
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/193]如图所示,一个矩形线框从匀强磁场的上方自由落下,进入匀强磁场中后,再从磁场中穿出。匀强磁场区域的宽度L大于线框的高度h。已知框的下边刚进入磁场时线框的...
参考答案:
| ABC |
参考解析:
无
【简答题】

[2/193]发电机是把其他形式的能转化为电能的机器,位于琼海万泉河上的牛路岭水电站发电过程主要是把_________能转化为电能;澄迈马村火力发电厂的发电过程主要...
参考答案:
| 机械;内(或热);核 |
参考解析:
无
【简答题】

[3/193]质量为M的小车置于光滑水平面上。小车的上表面由1/4圆弧和平面组成,车的右端固定有一不计质量的弹簧,圆弧A部分光滑,半径为R,平面BC部分粗糙,长为l...
参考答案:
解:(1)滑块与小车初始状态为静止,未状态滑块相对小车静止,即两者共速且速度为0,据能量守恒:mgR=μmg·2l,故 (2)弹簧压缩到最大形变量时,滑块与小车又一次共速,且速度均为0,此时,据能量守恒,弹簧的弹性势能  (3)弹簧与滑块刚分离的时候,弹簧的弹性势能为0,设此时滑块速度为v1,小车速度为v2,据能量守恒有  又因为系统动量守恒,有:mv1-Mv2=0 解得:  |
参考解析:
无
【简答题】

[4/193]如图所示,A、B是两块竖直放置的平行金属板,相距为2L,分别带有等量的正、负电荷,在两板间形电场强度大小为E匀强电场。A板上有一小孔(它的存在对两板间...
参考答案:
解:(1)当P由静止开始释放到弹簧第一次压缩到最左边的过程中,根据能的转化和守恒定律可得弹性势能: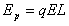 (2)分析知,小球每次离开Q时的速度大小相同,等于小球第一次与Q接触时速度大小v,根据动能定理可得: 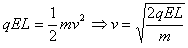 设小球与薄板Q碰撞n次后恰好向右运动到B板,则: 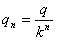 小球与薄板Q碰撞n次后向右运动从与Q分离到恰好到达B板的过程中,根据动能定理可得: 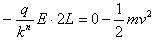 由以上几式可得:  (或取 (或取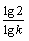 的整数) 的整数)(3)设小球第1次弹回两板间后向右运动最远距A板的距离为L1,则: 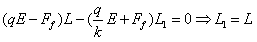 设小球第2次弹回两板间后向右运动最远距A板的距离为L2,则:  而此时电场力: 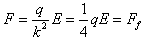 ,即带电小球可保持静止 ,即带电小球可保持静止所以带电小球初、末状态的电势能变化量: 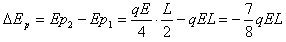 |
参考解析:
无
【简答题】

[5/193]电机带动水平传送带以速度v匀速传动,一质量为m的小木块由静止轻放在传送带上(传送带足够长 【图片】),若小木块与传送带之间的动摩擦因数为μ,如图所示,...
参考答案:
| 解:(1)小木块的加速度a=μg 小木块的位移l1=  (2) 小木块加速运动的时间t=  传送带在这段时间内位移l2=vt=  (3)小木块获得的动能Ek=  mv2 mv2(4)因摩擦而产生的热等于摩擦力(f)乘以相对位移(ΔL),故Q=f·ΔL=μmg(l2-l1)=  mv2 mv2(注:Q=Ek,但不是所有的问题都这样) (5)由能的转化与守恒定律得,电机输出的总能量转化为小木块的动能与摩擦热,所以E=Ek+Q=  mv2 mv2 |
参考解析:
无
【简答题】

[6/193]如图所示,水平传送带以恒定的速率v=4m/s运送质量为m=0.5kg的工件,工件都是在位置A处无初速地放在传送带上的,工件与传送带间的动摩擦因数μ=0...
参考答案:
|
解:(1)工件经t= |
参考解析:
无
【简答题】

[7/193]如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧一直保持竖直),下列关于能的叙述正确的是( &nb...
参考答案:
| B |
参考解析:
无
【简答题】

[8/193]斜面的高是0.6m,倾角是30°,质量为1kg的物体由顶端滑到底端.已知动摩擦因数是0.5,取g= 10 m/s2 ,在这个过程中产生____J 热量...
参考答案:
 |
参考解析:
无
【简答题】

[9/193]某海湾共占面积1.0×107 m2 ,涨潮时水深20 m ,此时关闭水坝闸门可使水位保持20 m 不变,退潮时,坝外水位降至18 m. 假如利用此水坝...
参考答案:
| 解:由于坝外面积很大,所以水量变化不影响水位高度, 本题相当于让高度为18 m ~20 m的这部分水平铺到坝外高度为18 m的水面上去, 这些水的重心只降低了1m , 即从 19 m 降到18 m ,每天涨潮两次, 所以产生的电能为   |
参考解析:
无
【简答题】

[10/193]一根轻弹簧,上端固定,下端拴一个重物P,处于静止状态,如图,现有外力把它向下拉一段距离,则以下说法错误的是( ) A.向下拉的某段过程中,重力势能的...
参考答案:
| ABC |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫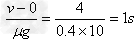 时间在传送带上滑动后和传送带达到相同速度;
时间在传送带上滑动后和传送带达到相同速度;