
创建自己的小题库
搜索

同角三角函数的基本关系式题库
题数
2000
考试分类
高中数学>同角三角函数的基本关系式
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-同角三角函数的基本关系式
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]若sinαcosα=18,且π4<α< π2,则sinα-cosα=( ) A.-34B.-32C.34D.32
参考答案:
∵
将sinαcosα=
则sinα-cosα=
故选D |
参考解析:
π4
【简答题】

[2/2000]已知tanθ= 43,则sinθ+cosθsinθ-cosθ的值为( ) A.13B.- 13C.7D.-7
参考答案:
=
=
=7 故答案选C |
参考解析:
sinθ+cosθsinθ-cosθ
【简答题】

[3/2000]若sinα+cosα=- 15,且0<α<π,则tanα的值是( ) A.- 34或- 43B.43C.- 43D.- 34
参考答案:
sinα+cosα=-
0<α<π,所以(sinα+cosα)2=
2sinαcosα=-
0<α<π∴sinα-cosα=
解①②得sinα=
故选D. |
参考解析:
15
【简答题】

[4/2000].若 【图片】,则 【图片】 .
参考答案:

|
参考解析:
解:因为
 ,
,

 ,
,

【简答题】

[5/2000]若tan160°=a,则sin2000°等于( ) A.a1+a2B.a1+a2C.11+a2D.-11+a2
参考答案:
| tan160°=tan(180°-20°)=-tan20°=a<0,得到a<0,tan20°=-a ∴cos20°=
∴sin20°=
则sin2000°=sin(11×180°+20°)=-sin20°=
故选B. |
参考解析:
无
【简答题】

[6/2000]已知 【图片】,且 【图片】,那么 【图片】等于 &nb...
参考答案:
|
D
|
参考解析:
无
【简答题】

[7/2000]已知cos(π-θ)=b,-1<b<1,b为实常数,则sin2θcot θ2的值为______.
参考答案:
| ∵cos(π-θ)=b,-1<b<1,b为实常数, ∴cosθ=-b,则sin2θcot
故答案为-2b+2b2. |
参考解析:
无
【简答题】

[8/2000]已知-π2<x<0,sinx+cosx= 15.求sinx-cosx的值.
参考答案:
∵-
又sinx+cosx=
∴sin2x=-
又∵sinx-cosx<0, ∴sinx-cosx=-
|
参考解析:
无
【简答题】

[9/2000]已知方程2x2-4x•sinθ+3cosθ=0的两个根相等,且θ为锐角,求θ和这个方程的两个根.
参考答案:
| 由题意得△=b2-4ac=(-4sinθ)2-4•2•3cosθ=0, 即16sin2θ-24cosθ=0, ∴16(1-cos2θ)-24cosθ=0, ∴2cos2θ+3cosθ-2=0, 解得cosθ=
又θ为锐角,∴θ=60°. 因此,原方程可化为 2x2-2
解得相等的二根为
|
参考解析:
12
【简答题】

[10/2000]已知 【图片】、 【图片】是方程 【图片】的两根,且 【图片】、 【图片】终边互相垂直. 求 【图片】的值.
参考答案:

|
参考解析:
设
 则
则
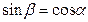 ,
,
由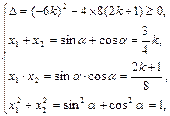 解知
解知
 .
.
 则
则
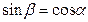 ,
,
由
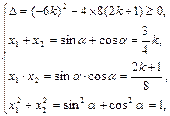 解知
解知
 .
.

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





