
创建自己的小题库
搜索

数学归纳法证明不等式题库
题数
335
考试分类
高中数学>数学归纳法证明不等式
售价
¥20
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-数学归纳法证明不等式
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/335]若不等式 【图片】对一切正整数n都成立,求正整数a的最大值,并用数学归纳法证明你的结论。
参考答案:
解:当n=1时, , ,即  ,即a<26, ,即a<26,又a∈N*, ∴取a=25, 下面用数学归纳法证明:  , ,(1)当n=1时,已证。 (2)假设当n=k时,  成立, 成立,则当n=k+1时,有     , ,∵  , ,∴  成立; 成立;由(1)、(2)可知,对一切n∈N*,都有不等式  成立。 成立。 ∴a的最大值为25。 |
参考解析:
无
【简答题】

[2/335]用数学归纳法证明: 【图片】.
参考答案:
|
证明:(1)当
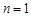 时,左边 时,左边
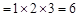 ,右边 ,右边
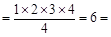 左边,∴等式成立. 左边,∴等式成立.
(2)设当 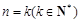 时,等式成立, 时,等式成立,
即 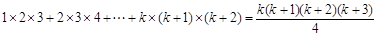 . 则当 . 则当
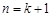 时, 时,
左边 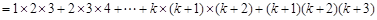
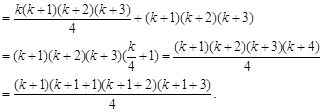
∴ 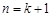 时,等式成立. 时,等式成立.
由(1)、(2)可知,原等式对于任意 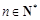 成立. 成立.
|
参考解析:
首先证明当n=1时等式成立,再假设n=k时等式成立,得到等式
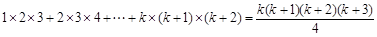 ,
,
下面证明当n=k+1时等式左边
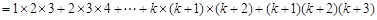 ,
,
根据前面的假设化简即可得到结果,最后得到结论.
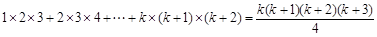 ,
,
下面证明当n=k+1时等式左边
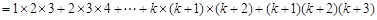 ,
,
根据前面的假设化简即可得到结果,最后得到结论.
【简答题】

[3/335]用数学归纳法证明“n 3+(n+1) 3+(n+2) 3(n∈N *)能被9整除”,要利用归纳假设证n=k+1时的情况,只需展开( ) A.(k+3...
参考答案:
|
A
|
参考解析:
假设当n=k时,原式能被9整除,
即k 3+(k+1) 3+(k+2) 3能被9整除.
当n=k+1时,(k+1) 3+(k+2) 3+(k+3) 3为了能用上面的归纳假设,只需将(k+3) 3展开,让其出现k 3即可.
即k 3+(k+1) 3+(k+2) 3能被9整除.
当n=k+1时,(k+1) 3+(k+2) 3+(k+3) 3为了能用上面的归纳假设,只需将(k+3) 3展开,让其出现k 3即可.
【简答题】

[4/335]用数学归纳法证明不等式: 【图片】>1(n∈N *且n>1).
参考答案:
|
见解析
|
参考解析:
①当n=2时,左边=
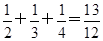 >1,
>1,
∴n=2时不等式成立;
②假设当n=k(k≥2)时不等式成立,即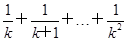 >1,
>1,
那么当n=k+1时,
左边=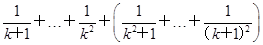
=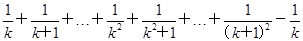
>1+(2k+1)·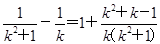 >1.
>1.
综上,对于任意n∈N *,n>1不等式均成立,原命题得证.
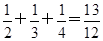 >1,
>1,
∴n=2时不等式成立;
②假设当n=k(k≥2)时不等式成立,即
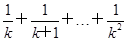 >1,
>1,
那么当n=k+1时,
左边=
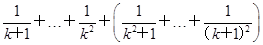
=
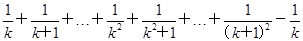
>1+(2k+1)·
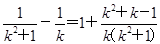 >1.
>1.
综上,对于任意n∈N *,n>1不等式均成立,原命题得证.
【简答题】

[5/335](本小题10分) 证明: 【图片】,其中 【图片】.
参考答案:
|
略
|
参考解析:
略
【简答题】

[6/335]是否存在常数a、b、c使等式1•(n2-12)+2(n2-22)+…+n(n2-n2)=an4+bn2+c对一切正整数n成立?证明你的结论.
参考答案:
分别用n=1,2,3代入解方程组
下面用数学归纳法证明. (1)当n=1时,由上可知等式成立; (2)假设当n=k时,等式成立, 则当n=k+1时,左边=1•[(k+1)2-12]+2[(k+1)2-22]+…+k[(k+1)2-k2]+(k+1)[(k+1)2-(k+1)2] =1•(k2-12)+2(k2-22)++k(k2-k2)+1•(2k+1)+2(2k+1)+…+k(2k+1) =
=
∴当n=k+1时,等式成立. 由(1)(2)得等式对一切的n∈N*均成立. |
参考解析:
| a+b+c=0 |
| 16a+4b+c=3 |
| 81a+9b+c=18 |
【简答题】

[7/335]各项均为正数的数列 【图片】对一切 【图片】均满足 【图片】.证明: (1) 【图片】; (2) 【图片】.
参考答案:
|
(1)详见解析,(2)详见解析.
|
参考解析:
(1)作差证明不等式,因为
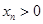 ,
,
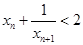 ,所以
,所以
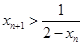 ,且
,且
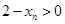 .
.
因此
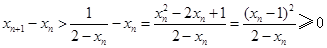 .即
.即
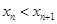 .(2)本题证明:
.(2)本题证明:
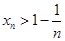 用数学归纳法,而证明
用数学归纳法,而证明
 用反证法. ① 当
用反证法. ① 当
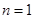 时,由题设
时,由题设
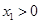 可知
可知
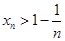 成立;② 假设
成立;② 假设
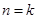 时,
时,
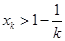 ,
,
当
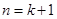 时,由(1)得,
时,由(1)得,
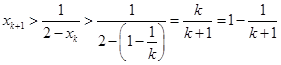 .由①,②可得,
.由①,②可得,
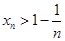 .假设存在自然数
.假设存在自然数
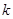 ,使得
,使得
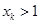 ,则一定存在自然数
,则一定存在自然数
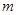 ,使得
,使得
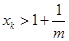 .因为
.因为
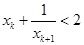 ,
,
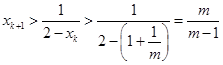 ,
,
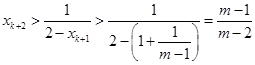 , ,
, ,
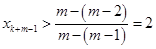 ,与题设
,与题设
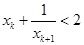 矛盾,所以,
矛盾,所以,
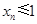 .若
.若
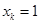 ,则
,则
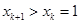 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.
【证明】(1)因为
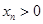 ,
,
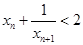 ,与题设
,与题设
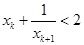 矛盾,所以,
矛盾,所以,
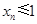 .若
.若
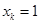 ,则
,则
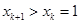 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.
所以
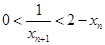 ,
,
所以
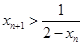 ,且
,且
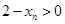 .
.
因为
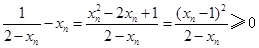 .
.
所以
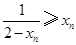 ,
,
所以
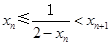 ,即
,即
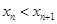 . 4分
. 4分
(注:用反证法证明参照给分)
(2)下面用数学归纳法证明:
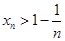 .
.
① 当
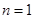 时,由题设
时,由题设
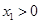 可知结论成立;
可知结论成立;
② 假设
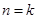 时,
时,
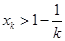 ,
,
当
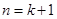 时,由(1)得,
时,由(1)得,
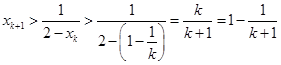 .
.
由①,②可得,
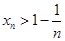 . 7分
. 7分
下面先证明
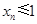 .
.
假设存在自然数
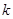 ,使得
,使得
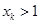 ,则一定存在自然数
,则一定存在自然数
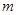 ,使得
,使得
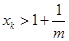 .
.
因为
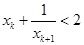 ,
,
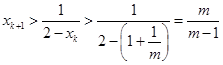 ,
,
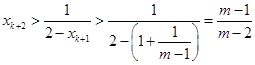 , ,
, ,
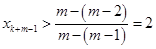 ,
,
与题设
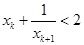 矛盾,所以,
矛盾,所以,
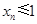 .
.
若
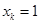 ,则
,则
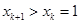 ,根据上述证明可知存在矛盾.
,根据上述证明可知存在矛盾.
所以
 成立. 10分
成立. 10分
【简答题】

[8/335]用数学归纳法证明不等式 【图片】的过程中, 由 【图片】递推到 【图片】时的不等式左边( ) A.增加了...
参考答案:
|
C
|
参考解析:
解:因为当n=k时,左边为

当n=k+1时,则左边为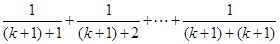
可见左边的变化为选C

当n=k+1时,则左边为
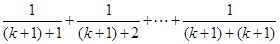
可见左边的变化为选C
【简答题】

[9/335]已知 【图片】, 【图片】是函数 【图片】的两个零点,其中常数 【图片】, 【图片】,设 【图片】. (Ⅰ)用 【图片】, 【图片】表示 【图片】, ...
参考答案:
|
(Ⅰ)
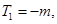
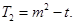 (Ⅱ)详见解析,(Ⅲ)详见解析. (Ⅱ)详见解析,(Ⅲ)详见解析.
|
参考解析:
(Ⅰ)由题意得:
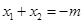 ,
,
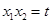 .因为
.因为
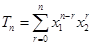 ,所以
,所以
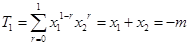 .
.
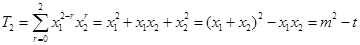 .对抽象的求和符号具体化处理,是解答本题的关键.(Ⅱ)
.对抽象的求和符号具体化处理,是解答本题的关键.(Ⅱ)
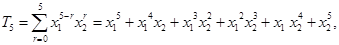 而
而
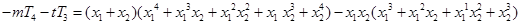
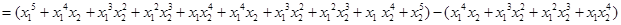
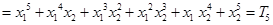 ,(Ⅲ)用数学归纳法证明有关自然数的命题. (1)当
,(Ⅲ)用数学归纳法证明有关自然数的命题. (1)当
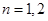 时,由(Ⅰ)问知
时,由(Ⅰ)问知
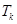 是整数,结论成立.(2)假设当
是整数,结论成立.(2)假设当
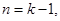
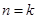 (
(
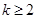 )时结论成立,即
)时结论成立,即
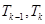 都是整数,由(Ⅱ)问知
都是整数,由(Ⅱ)问知
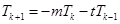 .即
.即
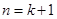 时,结论也成立.
时,结论也成立.
解:(Ⅰ)由
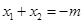 ,
,
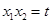 .
.
因为
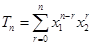 ,所以
,所以
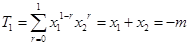 .
.
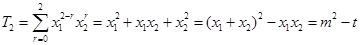 . 3分
. 3分
(Ⅱ)由
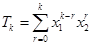 ,得
,得
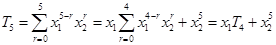 .
.
即
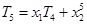 ,同理,
,同理,
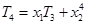 .
.
所以
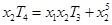 .
.
所以
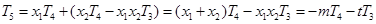 . 8分
. 8分
(Ⅲ)用数学归纳法证明.
(1)当
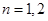 时,由(Ⅰ)问知
时,由(Ⅰ)问知
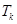 是整数,结论成立.
是整数,结论成立.
(2)假设当
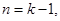
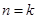 (
(
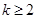 )时结论成立,即
)时结论成立,即
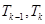 都是整数.
都是整数.
由
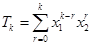 ,得
,得
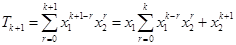 .
.
即
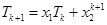 .
.
所以
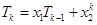 ,
,
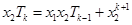 .
.
所以
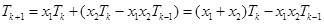 .
.
即
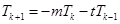 .
.
由
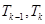 都是整数,且
都是整数,且
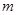 ,
,
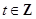 ,所以
,所以
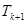 也是整数.
也是整数.
即
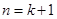 时,结论也成立.
时,结论也成立.
由(1)(2)可知,对于一切
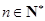 ,
,
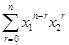 的值都是整数. 13分
的值都是整数. 13分
【简答题】

[10/335]已知f(n)=1+ 【图片】n∈N ),g(n)=2( 【图片】-1)(n∈N ). (1)当n=1,2,3时,分别比较f(n)与g(n)的大小(...
参考答案:
|
(1)当n=1时,f(1)>g(1);当n=2时,f(2)>g(2);当n=3时,f(3)>g(3).(2)f(n)>g(n)(n∈N
*),
|
参考解析:
(1)当n=1时,f(1)>g(1);当n=2时,f(2)>g(2);当n=3时,f(3)>g(3).
(2)猜想:f(n)>g(n)(n∈N *),即1+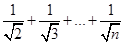 >2(
>2(
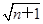 -1)(n∈N
*).
-1)(n∈N
*).
下面用数学归纳法证明:①当n=1时,f(1)=1,g(1)=2(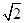 -1),f(1)>g(1).
-1),f(1)>g(1).
②假设当n=k时,猜想成立,即1+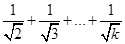 >2(
>2(
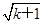 -1).
-1).
则当n=k+1时,f(k+1)=1+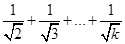 +
+
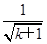 >2(
>2(
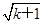 -1)+
-1)+
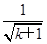 =2
=2
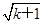 +
+
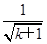 -2,而g(k+1)=2(
-2,而g(k+1)=2(
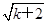 -1)=2
-1)=2
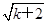 -2,
-2,
下面转化为证明: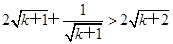 .
.
只要证:2(k+1)+1=2k+3>2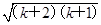 ,
,
需证:(2k+3) 2>4(k+2)(k+1),即证:4k 2+12k+9>4k 2+12k+8,此式显然成立.
所以,当n=k+1时猜想也成立.综上可知:对n∈N *,猜想都成立,
即1+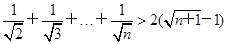 (n∈N
*)成立.
(n∈N
*)成立.
(2)猜想:f(n)>g(n)(n∈N *),即1+
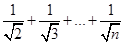 >2(
>2(
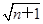 -1)(n∈N
*).
-1)(n∈N
*).
下面用数学归纳法证明:①当n=1时,f(1)=1,g(1)=2(
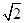 -1),f(1)>g(1).
-1),f(1)>g(1).
②假设当n=k时,猜想成立,即1+
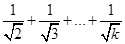 >2(
>2(
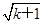 -1).
-1).
则当n=k+1时,f(k+1)=1+
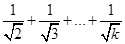 +
+
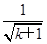 >2(
>2(
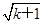 -1)+
-1)+
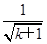 =2
=2
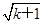 +
+
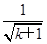 -2,而g(k+1)=2(
-2,而g(k+1)=2(
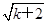 -1)=2
-1)=2
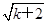 -2,
-2,
下面转化为证明:
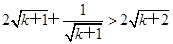 .
.
只要证:2(k+1)+1=2k+3>2
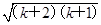 ,
,
需证:(2k+3) 2>4(k+2)(k+1),即证:4k 2+12k+9>4k 2+12k+8,此式显然成立.
所以,当n=k+1时猜想也成立.综上可知:对n∈N *,猜想都成立,
即1+
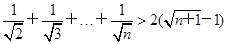 (n∈N
*)成立.
(n∈N
*)成立.

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





