
创建自己的小题库
搜索

电磁感应现象中的切割类问题题库
题数
954
考试分类
高中物理>电磁感应现象中的切割类问题
售价
¥25
 手机预览
手机预览
收藏
分享
去刷题
简介
高中物理-电磁感应现象中的切割类问题
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/954]如图所示为水平面内的两条相互平行的光滑金属导轨,电阻可以忽略不计,轨道间距为l。导轨所处水平面内存在着竖直方向的匀强磁场,磁感应强度为B。两导体杆a和...
参考答案:
|
(1)根据楞次定律,a杆受向左的安培力向右作减速运动,b杆受向右的安培力向右作加速运动,两杆受力等大反向,因此两杆系统动量守恒。当a杆的速度为v
1=v
0/2时,b杆的速度设为v
2,有
mv 1+2mv 2=mv 0 (2 分) 可得v 2= v 0/4 根据感应电动势规律可得此时两杆电动势 E 1=Blv 1=  Blv
0 Blv
0
E 2=Blv 2=  Blv
0 Blv
0
根据闭合回路欧姆定律,回路电路为 
I= 
根据安培力性质,两杆所受安培力大小为 F=BIl=  (2分) (2分)
根据牛顿第二定律,两杆加速度大小分别为 a 1=  = =
 ,a
2= ,a
2=
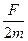 = =
 (2分) (2分)
(2)由于两杆的动能通过电磁感应转化为电能且由焦耳热方式放出,根据能量守恒,电路放出内能 Q=  = =
 (2分) (2分)
因为两杆电流在任意时刻都相等,所以两杆发热量与电阻成正比,两杆分别产生热量 Q 1=  = =

Q 2= 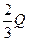 = =
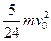 (1分) (1分)
(3)由安培力性质,杆受到的安培力 F=BIl 在一段很短的时间Δt内,由于电流可看做稳定,安培力产生冲量 Δτ="FΔt=BlΔq " (2分) 其中Δq为时间Δt内通过电路的电量,因为B、l都不变,所以即使在较长时间内此式结果仍成立。 又根据动量定理,a杆受到的安培力冲量大小为 τ=mv 0-mv 1= 
所以通过a杆的总电量 q=  = =
 (1分) (1分)
由法拉第电磁感应定律,电路中的总电动势 E= 
其中ΔS为电路面积的变化量,Δt为一段很短的时间 由闭合回路欧姆定律,电路中电流 I= 
由电流与电量关系 Δq=IΔt 根据以上三式可得 Δq=  (2分) (2分)
因为B、r都不变,所以此式在一段较长时间内仍成立,因此电路面积增加量为 S= 
两杆间距增加 x=  (1分) (1分)
|
参考解析:
略
【简答题】

[2/954]如图所示,P、Q为水平面内平行放置的光滑金属长直导轨,间距为L1,处在竖直向下、磁感应强度大小为B1的匀强磁场中,一导体杆ef垂直于P、Q放在导轨上,...
参考答案:
| 解:(1)设通过正方形金属框的总电流为I,ab边的电流为Iab,dc边的电流为I,有 Iab= 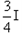 ① ①Idc=  ② ②金属框受重力和安培力,处于静止状态,有mg=B2IabL2+B2IdcL2 ③ 由①~③,解得I=  ④ ④(2)由(1)可得I= 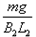 ⑤ ⑤设导体杆切割磁感线产生的电动势为E,有E=B1L1v ⑥ 设ad、dc、cb三边电阻串联后与ab边电阻并联的总电阻为R,则R= 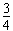 r ⑦ r ⑦根据闭合电路欧姆定律,有I=  ⑧ ⑧ 由⑤~⑧,解得v=  ⑨ ⑨ |
参考解析:
无
【简答题】

[3/954]2008北京奥运会上100 m赛跑跑道两侧设有跟踪仪,其原理如图所示,水平面上两根足够长的金属导轨平行固定放置,间距为 L="0.5" m,一端通过导...
参考答案:
|
BCD
|
参考解析:
由图象可知选项A错误,C正确
 ;由
;由
 及
及
 可得:
可得:
 ,从图象上分别读出两组
,从图象上分别读出两组
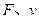 数据代入上式即可求得
B=1T,
数据代入上式即可求得
B=1T,
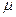 =0.4,所以BD正确。
=0.4,所以BD正确。
 ;由
;由
 及
及
 可得:
可得:
 ,从图象上分别读出两组
,从图象上分别读出两组
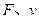 数据代入上式即可求得
B=1T,
数据代入上式即可求得
B=1T,
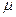 =0.4,所以BD正确。
=0.4,所以BD正确。
【简答题】

[4/954]如图所示,两根平行放置的竖直导电轨道处于匀强磁场中,轨道平面与磁场方向垂直。当接在轨道间的开关S断开时,让一根金属杆沿轨道下滑(下滑中金属杆始终与轨道...
参考答案:
| D |
参考解析:
无
【简答题】

[5/954]如图所示,水平放置的光滑平行金属导轨上有一质量为m的金属棒ab。导轨的一端连接电阻R,其他电阻均不计,磁感应强度为B的匀强磁场垂直于导轨平面向下,金属...
参考答案:
|
CD
|
参考解析:
随着ab运动速度的增大,安培力增大,由F-BIL=ma可知加速度减小,A错;如果导体棒速度增大,外力F对ab做的功等于电路中产生的电能与动能变化量之和,B错;当ab做匀速运动时,由动能定理可知外力F做功的功率等于电路中的电功率,C对;同理由功能关系可知无论ab做何种运动,它克服安培力做的功一定等于电路中产生的电能,D对,故选CD
点评:本题难度较小,巧妙应用动能定理和功能关系,克服安培力做了多少功就有多少电能产生
【简答题】

[6/954]如图所示,两根足够长的光滑平行金属导轨MN、PQ间距离L=0.5m,其电阻不计,两导轨及其构成的平面与水平面成30°角。完全相同的两金属棒ab、cd分...
参考答案:
|
(1) I=1A 电流方向由d至c (2) F=0.2N (3) v="2m/s"
|
参考解析:
(1)金属棒cd在安培力和重力导轨支持力作用下静止,正交分解后平行导轨方向有F
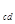 =mgsin30°金属棒cd受到的安培力F
=mgsin30°金属棒cd受到的安培力F
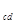 =BIL
=BIL
代入数据,解得I=1A
根据楞次定律可知,金属棒 cd中的电流方向由d至c
(2)金属棒ab与cd受到的安培力大小相等:F
 =F
=F
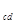
对金属棒ab,由共点力平衡有F=mgsin30°+F

代入数据解得F=0.2N
(3)金属棒发热功率P=I 2R
金属棒ab匀速运动的速度大小为v时,其产生的感应电动势E=BLv
由闭合电路欧姆定律知I=
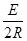
代入数据解得v=2m/s
【简答题】

[7/954]如图所示,间距为L、电阻为零的U形金属竖直轨道,固定放置在磁感应强度为B的匀强磁场中,磁场方向垂直纸面向里。竖直轨道上部套有一金属条bc,bc的电阻为...
参考答案:
解:(1)物体m自由下落与金属条碰撞的速度为 设物体m落到金属条2m上,金属条立即与物体有相同的速度v开始下落,由m和2m组成的系统相碰过程动量守恒  则  此时金属条以速度v向下滑动,切割磁感线,则金属条所受安培力为  对于金属条和物体组成的整体,由牛顿第二定律可得  联立解得金属条开始运动时的加速度为  (2)金属条和物体以速度vm做匀速运动,此时金属条和物体受力平衡,则有   下落h的过程中,由能量守恒得  联立解得  |
参考解析:
无
【简答题】

[8/954]如图所示,半径为 r、电阻不计的两个半圆形光滑导轨并列竖直放置,导轨端口所在平面刚好水平。在轨道左上方端口M、N 间接有阻值为R 的小电珠,整个轨道处...
参考答案:
|
(1)
 ,方向水平向左(2)小电珠上产生的热量 ,方向水平向左(2)小电珠上产生的热量
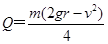
|
参考解析:
(1)根据右手定则可判电流方向,再根据左手定则判断安培力的方向,对棒受力分析.
(2)根据能量守恒计算:金属棒减少的重力势能转换为电路的电能和金属棒的动能.
解:(1)由右手定则可判:电流方向由N到M,由左手定则可知ab棒收到的安培力F,方向水平向左
在最低点ab棒切割磁力线产生的电动势为:E=BLv…①
由闭合电路欧姆定律得:
 …②
…②
由F=BIL,联立①②可得
 .
.
(2)在ab棒下滑的过程中设小灯泡上产生的热量为Q,则整个电路上产生的热量为2Q,
由能量守恒定律得:
 .
.
解得:
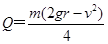 .
.
【简答题】

[9/954](12分).如图所示,水平面上有一个动力小车,在动力小车上竖直固定着一个长度L 1、宽度L 2的矩形线圈,线圈匝线为n,总电阻为R,小车和线圈的总质量...
参考答案:
|
(1)
 , ,
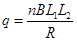 ; ;
(2) 
(3)  ,( ,(
 ) )
|
参考解析:
(1)线圈全部进入磁场时速度:

最大电动势:

最大电流为:

导线横截面的电量:

(2)设进入和离开磁场过程中,线圈产生的焦耳热分别为
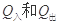 ,则在整个过程中,
,则在整个过程中,
牵引力的总功:

 ,
,
 ;将
;将
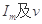 代入
代入
得:

解得:

(3)①小车进入磁场阶段做匀加速运动:
 ,
,
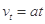 ,
,
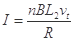
由
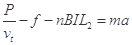 得:
得:
 ,(
,(
 )
)
②小车完全在磁场中运动:
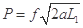 ,(
,(
 )
)
③小车匀速穿出磁场的过程:

得:
 ,(
,(
 )。
)。
【简答题】

[10/954]如图,在竖直面内有两平行金属导轨AB、CD。导轨间距为L,电阻不计。一根电阻不计的金属棒 【图片】可在导轨上 【图片】无摩擦地滑动。棒与导轨垂直,并接...
参考答案:
|
棒匀速向左运动
 ,感应电流为顺时针方向,电容器上板带正电。 ,感应电流为顺时针方向,电容器上板带正电。
∵微粒受力平衡,电场力方向向上,场强方向向下 ∴微粒带负电 
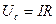


由以上各式求出 
|
参考解析:
略

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





