创建自己的小题库
搜索
向心力题库
题数
2000
考试分类
高中物理>向心力
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中物理-向心力
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/2000]如图所示，两质量相同的小球A、B，分别用细线悬挂于等高的两点，A球的悬线比B球的长，把两球均拉到悬线水平后将小球由静止释放，以悬点所在平面为参考平面，...
参考答案：
A、根据动能定理mgL=
B、根据动能的表达式EK=
C、A、B两球在运动的过程中，只有重力做功，机械能守恒，初始位置的机械能相等，所以在最低点，两球的机械能相等．故C正确． D、在最低点，根据牛顿第二定律得： F-mg=m
得F=mg+m
故选CD |
参考解析：
12
【简答题】
[2/2000]如图所示，一半径为R的绝缘圆形轨道竖直放置，圆轨道最低点与一条水平轨道相连，轨道都是光滑的，轨道所在空间存在水平向右的匀强电场，从水平轨道上的A点由静...
参考答案：
| （1）从A→C过程，根据动能定理得： qE•4R-mg•2R=
又：qE=
联立解得：vC=
（2）在C点，由牛顿第二定律得： N+mg=m
代入解得：N=0 答：（1）小球的速度为
（2）轨道对小球的弹力为零． |
参考解析：
12
【简答题】
[3/2000]如 【图片】图所示，A、B两小球质量相同，用轻线把它们连结，并跨过两个无摩擦的定滑轮。在B球左右摆动的时候，则A球将 【图片】 [ &nbs...
参考答案：
| C |
参考解析：
无
【简答题】
[4/2000]为使汽车安全转弯，以下做法可取的是（ ） A．遇到弯道应当加快速度通过B．遇到弯道应当减速通过C．建造公路时，弯道内侧要比外侧高D．建造公路时，弯道...
参考答案：
| A、B汽车在圆弧水平弯道路面行驶，做圆周运动，其所需要的向心力由静摩擦力提供，则： F静=m
由上式可知，当静摩擦力越大时，速度也越大．所以静摩擦力最大时，速度达最大．当速度继续增大时，静摩擦力不足以提供所需要的向心力，将做离心运动，所以为了安全转弯，必须减速，故A错误，B正确． C、D建造公路时，弯道内侧要比外侧低，速度恰当时，由重力和路面的支持力的合力提供向心力．故C错误，D正确． 故选：BD |
参考解析：
无
【简答题】
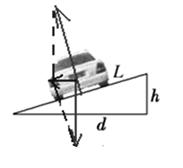
[5/2000]为获得汽车行驶各项参数，汽车测试场内有各种不同形式的轨道。如图所示。在某外高内低的弯道测试路段汽车向左拐弯，汽车的运动可看作是做半径为 【图片】的圆周...
参考答案：
|
B
|
参考解析：
把路基看做斜面，设其倾角为
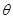，汽车在斜面上受到自身重力
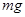和斜面支持力
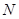，二者的 合力提供向心力，即指向水平方向。根据几何关系可得合力为
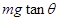，即向心力，所以
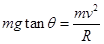计算得
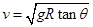，根据路基的高和水平宽度得
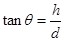，带入得
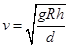答案B对。
【简答题】
[6/2000]如图所示，一根原长l = 0.1m的轻弹簧，一端挂一质量m =0.5 kg的小球，以另一端为圆心在光滑水平面上做匀速圆周运动，角速度ω=10rad／s...
参考答案：
| 解：设弹簧伸长Xm，则有弹簧弹力f=kX ， 弹簧提供小球以半径长为(l+X)，向心力为f=kX=mω2(l+X)，做匀速圆周运动。 代入数据解得： X=0.1m 。 |
参考解析：
无
【简答题】
[7/2000]如图所示，某物体沿 【图片】光滑圆弧轨道由最高点滑到最低点过程中，物体的速率逐渐增大，则( ) 【图片】A．物体的合力为零B．物体的合力大小不变，方...
参考答案：
|
D
|
参考解析：
据题知，物体做圆周运动，一定有外力提供向心力，合力一定不为零，故A错误；物体做圆周运动，一定有指向圆心的外力提供向心力，物体的速率增大，一定有沿圆弧切线方向的分力，根据平行四边形定则可知，物体的合力方向始终与其运动方向不垂直（最低点除外），故BC错误，D正确．故选：D
【简答题】
[8/2000]一辆汽车行驶到半径为R的圆弧形凸形桥最高点，已知汽车此时速度大小v0，为，汽车质量为m，重力加速度为g，则汽车在凸形桥最高点受到的桥面支持力是____...
参考答案：
| 设汽车在凸形桥最高点受到的桥面支持力为F，根据牛顿第二定律得： mg-F=m
得到F=mg-m
故本题答案是：F=mg-m
|
参考解析：
| v | 20 |
【简答题】
[9/2000]如图所示，轻杆长2L，中点装在水平轴O点，两端分别固定着小球A和B，A、B球质量分别为m、2m，整个装置在竖直平面内做圆周运动，当杆绕O转动到某一时刻...
参考答案：
| 解：设图示位置A、B两球速率为V，且杆对B球的作用力为F，即O轴所受作用力为F，则： 对A球有：mg=  …… （1）对B球有：F－2mg =2  …… （2） 由（1）（2）可求得：F=4mg |
参考解析：
无
【简答题】
[10/2000]如图所示，粗糙的半球体固定在水平面上，小物体恰好能沿球面匀速率下滑，则下滑过程中，小物体对球面的压力大小变化情况是（ ） A．一直增大B．一直减小C...
参考答案：
| 小物体做匀速圆周运动，合外力提供向心力，设重力与该点半径方向的夹角为θ，则有： mgcosθ-N=m
解得：N=mgcosθ-m
下滑时，θ增大，则mgcosθ减小，而m
故选：B |
参考解析：
无
