
创建自己的小题库
搜索

牛顿第二定律题库
题数
2000
考试分类
高中物理>牛顿第二定律
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中物理-牛顿第二定律
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]静止的传送带上有一砖块正在匀速下滑,此时开动传送带向上传送.那么物体滑到底端所用的时间与传送带不动时比较 【图片】A.下滑时间增大.B.下滑时间不变....
参考答案:
|
B
|
参考解析:
无
【简答题】

[2/2000]质量为m的带电小球用绝缘线悬挂于O点,并处于水平向右的大小为E的匀强电场中(设电场足够大),小球静止时,丝线与铅垂线夹角为θ,如图所示,求:(1)小球...
参考答案:
| (1)因小球向右偏,所受电场力向右,与电场强度方向相同,故带正电荷; (2)小球受力情况,如图所示. 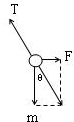 根据平衡条件得: qE=mgtanθ 得:q=
(3)如果将细线烧断,球沿合力方向做匀加速直线运动; 烧断细线后小球所受合外力为:F=
根据牛顿第二定律得加速度为:a=
答:(1)小球带正电荷; (2)小球电荷量为
(3)若将丝线烧断,小球的加速度为
|
参考解析:
无
【简答题】

[3/2000]空间存在竖直向上的匀强电场,质量为m的带正电的微粒水平射入电场中,微粒的运动轨迹如图所示,在相等的时间间隔内( ) 【图片】A...
参考答案:
|
C
|
参考解析:
带电粒子受到竖直向上的电场力和竖直向下的重力,电场力大于重力,合力也是恒力,方向竖直向上,因此粒子才向上偏转,根据牛顿第二定律,有
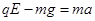 。带电粒子做类平抛运动,在竖直方向,相等的时间间隔内发生的位移之比为1:3:5:7 ,因此重力做功不相等,选项A错误。电场力做功也不相等,选项B错误。电场力做功大于重力做功,选项C正确,D错误。
。带电粒子做类平抛运动,在竖直方向,相等的时间间隔内发生的位移之比为1:3:5:7 ,因此重力做功不相等,选项A错误。电场力做功也不相等,选项B错误。电场力做功大于重力做功,选项C正确,D错误。
【简答题】

[4/2000](18分)如图所示为儿童乐娱乐的滑梯示意图,其中AB为长s 1=3m的斜面滑槽,与水平方向夹角为37 0,BC为水平滑槽,AB与BC连接处通过一段圆弧...
参考答案:
|
(1)
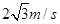 (2)1m (2)1m
|
参考解析:
解答本题的关键是要多次运用功能关系列式求解,同时应注意分析题意中的临界条件.
(1)小孩由A滑到B的过程,由能的转化和守恒:
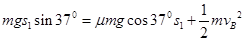
带入数据计算得,小孩到B时速度
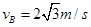
(2)儿童在C点若速度过大则重力不足以提供向心力将会做平抛运动.要使儿童不会做平抛(与接触面间压力不为零),则在C点儿童应做圆周运动,满足:
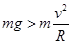
解得:
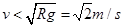 .
.
儿童从B到C处,根据能的转化和守恒:
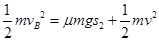
解得:
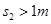
所以为了使该儿童滑下后不会从C处平抛出去,水平滑槽BC长度s 2应大于1m.
【简答题】

[5/2000]关于运动和力的关系,下列说法中正确的是( ) A.物体做曲线运动,其加速度一定在变化B.物体做曲线运动,...
参考答案:
|
B。
|
参考解析:
无
【简答题】

[6/2000]如图所示,放在水平地面上质量为M的小木块,木块与地面之间的动摩擦因数为μ,当地的重力加速度为g。在大小为F、方向与水平方向成α角的拉力作用下能够沿着地...
参考答案:
|
D
|
参考解析:
对物体进行受力分析:F
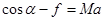
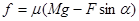
联立解得,a=(Fcosα+μFsinα-μMg)/M,选D.
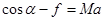
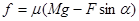
联立解得,a=(Fcosα+μFsinα-μMg)/M,选D.
【简答题】

[7/2000]如图甲所示,MN、PQ是相距d=l.0m足够长的平行光滑金属导轨,导轨平面与水平面间的夹角为 【图片】,导轨电阻不计,整个导轨处在方向垂直于导轨平面向...
参考答案:
|
(1)
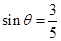 (2) (2)
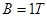
|
参考解析:
(1)S断开时ab做匀加速直线运动,根据图乙可得:
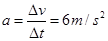
根据牛顿第二定律可得:
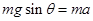 ,所以
,所以
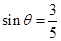
(2)
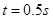 时S闭合,ab先做加速度减小的加速运动,当速度达到最大
时S闭合,ab先做加速度减小的加速运动,当速度达到最大
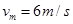 后做匀速直线运动,根据平衡条件有:
后做匀速直线运动,根据平衡条件有:
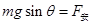 ,又因为
,又因为
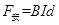 ,
,
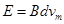 ,
,
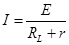 ,联立解得:
,联立解得:
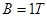
【简答题】

[8/2000]将一弹性绳(质量不计)一端固定在某一高处O点,另一端系在一个物体上,现将物体从O点处由静止释放,测出物体在不同时刻的速度V和该物体到O点的距离s,得到...
参考答案:
|
B
|
参考解析:
试题分析: 由图可知,当速度最大时,加速度等于零,此时重力等于弹簧弹力,则有:mg=k(20-12)解得:k=
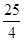 N/m,物体下落过程中弹性绳的最大拉力大小约为F
max= k(L-L
0)=150N,所以A错误;由图可知,弹性绳的最大拉力最大时,物体下落过程中加速度最大,由牛顿第二定律得a=20m/s
2所以B正确;当弹性绳上的拉力为100N,弹性绳形变量为16m,弹性绳长度就是28m,从图中读出对应的速度为:v=15.5m/s,故C错误;在下落的整个过程中,只有重力和弹性绳弹力做功,根据动能定理得:mgh-E
p=0-0,解得弹性绳弹性势能最大值约为1800J,故D错误的
N/m,物体下落过程中弹性绳的最大拉力大小约为F
max= k(L-L
0)=150N,所以A错误;由图可知,弹性绳的最大拉力最大时,物体下落过程中加速度最大,由牛顿第二定律得a=20m/s
2所以B正确;当弹性绳上的拉力为100N,弹性绳形变量为16m,弹性绳长度就是28m,从图中读出对应的速度为:v=15.5m/s,故C错误;在下落的整个过程中,只有重力和弹性绳弹力做功,根据动能定理得:mgh-E
p=0-0,解得弹性绳弹性势能最大值约为1800J,故D错误的
【简答题】

[9/2000]放在光滑水平面上的物体,在水平拉力F的作用下以加速度a运动,现将拉力F改为2F(仍然水平方向),物 体运动的加速度大小变为a'。则 [ &n...
参考答案:
| C |
参考解析:
无
【简答题】

[10/2000]如图所示,质量为m的小球A穿在绝缘杆上,细杆的倾角为α,小球A带正电,电荷量为q.在杆上B点处固定一个电荷量为Q的正电荷.将A由距B竖直高度为H处无初...
参考答案:
| (1)A球刚释放时,受到重力、沿细杆向上的库仑力和细杆的支持力,根据牛顿第二定律得: mgsinα-
得:a=gsinα-
(2)到达平衡位置时,速度最大,根据平衡条件,有: mgsinα-
得:x=
(3)从A到C过程,只有重力和电场力做功,根据动能定理,有: mgsinα•x+q•UAC=
将x代入,解得:UAC=
答:(1)A球刚释放时的加速度是gsinα-
(2)当A球的动能最大时,A球与B点的距离为
(3)A、C两点的电势差为
|
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





