
创建自己的小题库
搜索

理想气体状态方程题库
题数
761
考试分类
高中物理>理想气体状态方程
售价
¥25
 手机预览
手机预览
收藏
分享
去刷题
简介
高中物理-理想气体状态方程
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/761]如图所示为0.5mol某种气体的p~t图线,图中p0为标准大气压.则气体在标准状况下的体积是______ L,在B状态时的体积是______...
参考答案:
| 1mol任何气体在标准状况下的体积为22.4L,0.5mol某种气体在标准状况下的体积是11.2L. 根据气体状态方程
在P-T图象中等容线为过原点的直线,其中T为热力学温度温度. 所以在图中,虚线及延长线为等容线,A点的体积为11.2L. A到B,压强不变,根据气体状态方程
VB=14L. 故答案为:11.2,14 |
参考解析:
无
【简答题】

[2/761]【选修3-3选做题】 一气缸竖直倒放在水平地面上,缸体质量M=10 kg,活塞质量m=4 kg,活塞横截面积S=2×10-3 m2。活塞上面的气缸里封...
参考答案:
| 解:(1)在气体温度为127℃时,对活塞根据平衡条件有P0S=mg+P1S 在气缸内气体长度L2=24 cm时,对活塞根据平衡条件有P0S+k(L2-L1)=mg+p2S 根据气体状态方程有  代入解得T2=600K (2)当气体压强达到一定值时,气缸对地压力为零,此后再升高气体温度,气体压强不变,气体做等压变化。设气缸刚好对地没有压力时弹簧伸长量为△x,则k△x=(m+M)g 对气缸,根据平衡条件有p3S=Mg+P0S 根据气体状态方程有  各式联立解得T0=1012.5 K |
参考解析:
无
【简答题】

[3/761]A 组:一定质量理想气体,其状态沿图中的直线 ABC 进行变化,下列说法正确的是( ) A.tA=tB=tCB.tA=...
参考答案:
A、B根据气态方程
由于PAVA=PCVC<PBVB,所以得到:tA=tC<tB.故AB错误. C、D由
解得TB=360K 则得tB=360-273=87℃.故C错误,D正确 故选D |
参考解析:
PVT
【简答题】

[4/761]水平放置的汽缸被活塞分为体积相同的 A、 B两部分,活塞可以无摩擦自由移动且不漏气,气缸和活塞均用绝热材料制成. A、 B中分别装有等质量的同种理想气...
参考答案:
|
B
|
参考解析:
本题考查理想气体的状态方程;气体压强的微观意义。解答本题的关键是抓住A、B两部分的压强始终相同,根据气体状态方程
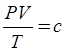 和已知的变化量去判断其它的物理量。
和已知的变化量去判断其它的物理量。
A、当A加热时,气体A的温度升高,压强增大,由于活塞与气缸壁的接触是光滑的,可以自由移动,所以A、B两部分的压强始终相同,都变大,故A错误;
B、由于A气体膨胀,B气体被压缩,所以外界对b气体做功,根据热力学第一定律得:b的温度也升高了,由
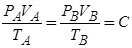 、
、
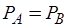 和
和
 可知,
可知,
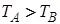 ,故B正确;
,故B正确;
C、由于A气体膨胀,B气体被压缩,最终A气体体积大于B气体体积,故C错误;
D、虽然加热后A的分子热运动比B的分子热运动更激烈,但
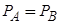 ,所以气体分子单位时间与活塞碰撞的次数相等,故D错误。
,所以气体分子单位时间与活塞碰撞的次数相等,故D错误。
因此选B。
【简答题】

[5/761]如图所示,U形管右管内径为左管内径的 【图片】倍,管内水银在左管内封闭了一段长为26cm、温度为280K的空气柱,左右两管水银面高度差为36cm,大气...
参考答案:
|
52;427
|
参考解析:
由理想气体状态方程
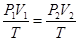 即
即
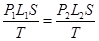
又P ="76" cmHg-36cmHg=40cmHg,所以
="76" cmHg-36cmHg=40cmHg,所以
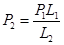 =52cmHg;
=52cmHg;
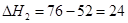 cmHg
cmHg
加热后气体增长6cm,所以有6cm水银柱进入右侧,因为右管内径为左管内径的 倍,右管横截面积是左管的2倍,所以右侧水银柱上升
倍,右管横截面积是左管的2倍,所以右侧水银柱上升
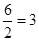 cm,所以P
cm,所以P
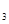 =76-(24-6-3)=61cmHg
=76-(24-6-3)=61cmHg
由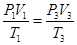 ,因为
,因为
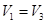 ,
,
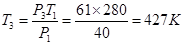
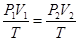 即
即
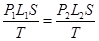
又P
 ="76" cmHg-36cmHg=40cmHg,所以
="76" cmHg-36cmHg=40cmHg,所以
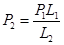 =52cmHg;
=52cmHg;
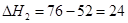 cmHg
cmHg
加热后气体增长6cm,所以有6cm水银柱进入右侧,因为右管内径为左管内径的
 倍,右管横截面积是左管的2倍,所以右侧水银柱上升
倍,右管横截面积是左管的2倍,所以右侧水银柱上升
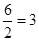 cm,所以P
cm,所以P
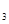 =76-(24-6-3)=61cmHg
=76-(24-6-3)=61cmHg
由
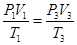 ,因为
,因为
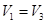 ,
,
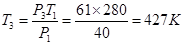
【简答题】

[6/761]薄膜材料气密性能的优劣常用其透气系数来加以评判。对于均匀薄膜材料,在一定温度下,某种气体通过薄膜渗透过的气体分子数 【图片】,其中t为渗透持续时间,S...
参考答案:
| 解:开始时U形管右管中空气的体积和压强分别为 V2=HA ① p2=p1 经过2小时,U形管右管中空气的体积和压强分别为  ② ② ③ ③渗透室下部连同U形管左管水面以上部分气体的总体积和压强分别为  ④ ④ ⑤ ⑤式中ρ为水的密度,g为重力加速度。由理想气体状态方程  可知,经过2小时,薄膜下部增加的空气的摩尔数 可知,经过2小时,薄膜下部增加的空气的摩尔数 ⑥ ⑥在2个小时内,通过薄膜渗透过去的分子数  ⑦,式中NA为阿伏伽德罗常量 ⑦,式中NA为阿伏伽德罗常量渗透室上部空气的摩尔数减少,压强下降,下降了△p  ⑧ ⑧经过2小时渗透室上部分中空气的压强为  ⑨ ⑨测试过程的平均压强差  ⑩ ⑩根据定义,由以上各式和有关数据,可求得该薄膜材料在0℃时对空气的透气系数  ⑾ ⑾ |
参考解析:
无
【简答题】

[7/761]一定质量的理想气体经历了从A→B→C温度缓慢升高的变化过程,如图所示,从A→B过程的p-T图象和从B→C过程的V-T图象各记录了其部分变化过程,试求:...
参考答案:
①由p-T图可知,
气体的温度升高,内能增大,根据热力学第一定律得知,气体将吸热. ②从B→C过程:
代入数据有
解得pc=1.25×105Pa 故答案为:①不做功,吸热;②气体在C状态时的压强为1.25×105Pa. |
参考解析:
无
【简答题】

[8/761]为了测量大米的密度,某同学根据如图所示实验装置,设计实验步骤如下:A.取适量的大米,用天平测出其质量,然后将大米装入注射器内;B.缓慢推动活塞至某一位...
参考答案:
| (1)气体在变化的过程中,气体的温度是不变的,所以气体做的是等温变化,所以本实验是根据玻意耳定律来设计的; (2)设大米的体积的为V0,对于封闭的气体有, 初状态 P1=1.60×106Pa,V1=1.37×10-3-V0, 末状态 P2=1.78×106Pa,V2=1.27×10-3-V0, 由玻意耳定律可得, P1V1=P2V2, 带入数据解得V0=3.8×10-3m3, 所以大米的密度为ρ=
(3)为了减小实验误差,可以采用图象法处理数据, 根据由玻意耳定律可得, PV=K 即P(V-V0)=K, 所以V=V0+K
所以可以通过绘制V-
故答案为:(1)玻意耳 (2)1.7×103 (3)重复步骤B,记录多个位置的刻度V和读取相应的气体压强p,
|
参考解析:
mV
【简答题】

[9/761]在湖面下50 m深处,温度为7℃,体积为1 cm 3的气泡,升到湖面,温度为17℃,体积将变为多大?(p 0="10" m水柱)
参考答案:
|
6.2 cm
3
|
参考解析:
在深处时
p 1=p 0+h="(10+50)" m="60" m水柱
V 1="1" cm 3
T 1="(273+7)" K="280" K
在湖面时p 2=p 0="10" m水柱
V 2=?
T 2=(273+17) K="290" K
根据理想气体状态方程: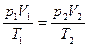
得V 2=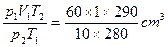 ="6.2" cm
3
="6.2" cm
3
p 1=p 0+h="(10+50)" m="60" m水柱
V 1="1" cm 3
T 1="(273+7)" K="280" K
在湖面时p 2=p 0="10" m水柱
V 2=?
T 2=(273+17) K="290" K
根据理想气体状态方程:
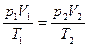
得V 2=
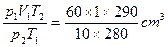 ="6.2" cm
3
="6.2" cm
3
【简答题】

[10/761]图为简易测温装置,玻璃管中一小段水银封闭了烧瓶内一定质量的气体,当温度升高时 【图片】A.瓶内气体的密度增大B.瓶内气体分子的平均动能增加C.外界对瓶...
参考答案:
|
BD
|
参考解析:
瓶内气体压强不变,根据理想气态方程,温度升高时,瓶内气体体积变大,对外做功,密度变小,所以AC错误。

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





