
创建自己的小题库
搜索

平面向量基本定理及坐标表示题库
题数
1277
考试分类
高中数学>平面向量基本定理及坐标表示
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-平面向量基本定理及坐标表示
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1277]如图,四边形OABC是边长为1的正方形,OD=3,点P为△BCD内(含边界)的动点,设OP=α OC+β OD(α,β∈R),则α+β的最大值等于__...
参考答案:
| 以O为原点,以OD所在直线为x轴建立直角坐标系, 设点P(x,y),∵
所以,x=3β,y=α,α+β=y+
由于点P在△BCD内(包含边界),目标函数为 α+β=y+
当点P为点B(1,1)时,α+β=y+
故答案为:
图(1) 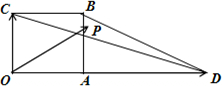 ,图(2) 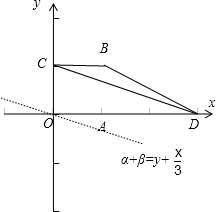 |
参考解析:
无
【简答题】

[2/1277]设向量 【图片】,向量 【图片】垂直于向量 【图片】,向量 【图片】平行于 【图片】,试求 【图片】的坐标.
参考答案:

|
参考解析:
无
【简答题】

[3/1277]将函数 【图片】的图像按平移向量 【图片】平移后得到函数 【图片】的图像,则该平移向量 【图片】=______。
参考答案:
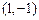
|
参考解析:
略
【简答题】

[4/1277]已知向量 【图片】= (-3 ,2 ) , 【图片】="(x," -4) , 若 【图片】// 【图片】,则x=( ...
参考答案:
|
C.
|
参考解析:
因为向量
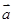 = (-3 ,2 ) ,
= (-3 ,2 ) ,
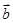 ="(x," -4) , 且
="(x," -4) , 且
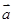 //
//
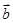 ,所以
,所以
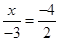 ,x=6,故选C。
,x=6,故选C。
点评:简单题,两向量平行,对应坐标成比例。
【简答题】

[5/1277]设向量 【图片】, 【图片】,则下列结论中正确的是( ) A. 【图片】B. 【图片】C. 【图片】与 【图片】垂直D. 【图片...
参考答案:
|
C
|
参考解析:
∵
 ,
,
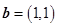 ,∴
,∴
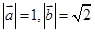 ,
,
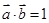 ,
,
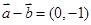 ,∴
,∴
 ,∴
,∴
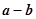 与
与
 垂直,故选C
垂直,故选C
点评:熟练掌握向量的坐标运算及数量积的定义、变形是解决此类问题的关键,属基础题
【简答题】

[6/1277]已知:A、B、C是 【图片】的内角, 【图片】分别是其对边长,向量 【图片】, 【图片】, 【图片】.求角A的大小;
参考答案:
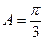
|
参考解析:
(Ⅰ)
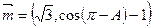 =
=
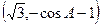
 =
=

∵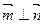
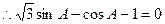
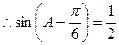
∵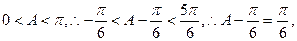
 .
.
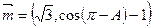 =
=
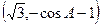
 =
=

∵
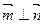
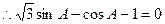
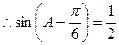
∵
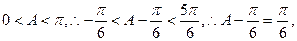
 .
.
【简答题】

[7/1277]已知向量m=(2x-2,2- 3y),n=( 3y+2,x+1),且m∥n, OM=(x,y)(O为坐标原点).(1)求点M的轨迹C的方程;(2)是否...
参考答案:
(1)∵向量
∴(2x-2)(x+1)-(2-
化简可得,点M的轨迹C的方程为
(2)设A(x1,y1),B(x2,y2), 由题意知l的斜率一定不为0,故不妨设l:x=my+1,代入椭圆方程,消元可得(2m2+3)y2+4my-4=0 ∴y1+y2=-
假设存在点P,使四边形OAPB为平行四边形,其充要条件为
∴P(x1+x2,y1+y2) ∴
∴2
∵A,B在椭圆上,∴2
∴2x1x2+3y1y2=-3 ∵y1+y2=-
∴m=±
当m=
∴
∴cos∠AOB=
∴sin∠AOB=
∴平行四边形OAPB的面积为|
当m=-
故存在存在点P,使四边形OAPB为平行四边形. |
参考解析:
m
【简答题】

[8/1277]已知a=(2,-1,3),b=(-1,4,-2),c=(7,7,λ),若a、b、c三向量共面,则实数λ等于( ) A.3B.5C.7D.9
参考答案:
∵
∴
∴(7,7,λ)=(2x,-x,+3x)+(-y,4y,-2y)=(2x-y,-x+4y,3x-2y), ∴2x-y=7,-x+4y=7,3x-2y=λ, 解得 λ=9; 故选D. |
参考解析:
a
【简答题】

[9/1277]已知向量 【图片】,则与向量 【图片】平行的一个单位向量是________.
参考答案:

|
参考解析:
设与向量
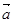 平行的单位向量是(x,y),则y=3x且
平行的单位向量是(x,y),则y=3x且
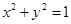 ,解得
,解得
 ,∴与向量
,∴与向量
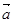 平行的一个单位向量是
平行的一个单位向量是

点评:熟练掌握向量的坐标运算及单位向量的定义是解决此类问题的关键
【简答题】

[10/1277](本小题满分12分)如图所示, 【图片】中, 【图片】, 【图片】, 【图片】, 【图片】(1)试用向量 【图片】, 【图片】来表示 【图片】. (2...
参考答案:
|
(1)
 (2) (2)
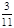 . .
|
参考解析:
(1)直接利用向量加法或减法的三角形法则表示即可.
(2)因为D、O、N三点共线,所以
 ,
,
又因为A,O,M三点共线,所以
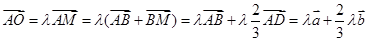
所以
 ,所以
,所以
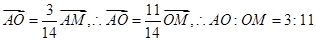 .
.
点评:根据平面向量的基本定理,平面内的任一向量都要可以用不共线的非零向量来表示,因而
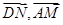 都可以用向量
都可以用向量
 ,
,
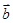 表示,在表示要用到向量的加减法计算法则。
表示,在表示要用到向量的加减法计算法则。
证明线段比值时如果它们是共线或平行时,可以利用向量共线定理解决。

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





