
创建自己的小题库
搜索

函数、映射的概念题库
题数
2000
考试分类
高中数学>函数、映射的概念
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-函数、映射的概念
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”,那么函数解析式为y=2x2+1,值域为{5,19}的“孪生函数”共有( ...
参考答案:
令2x2+1=5得x=±
即x=-
则“孪生函数”共有3×3=9个. 故选D. |
参考解析:
2
【简答题】

[2/2000]已知函数 【图片】的两个零点是2和3,则函数 【图片】的零点是( ) A. 【图片】和 【图片】B. 【图片】和 【...
参考答案:
|
C
|
参考解析:
无
【简答题】

[3/2000]对于函数 【图片】,若 【图片】使得 【图片】成立,则称 【图片】为 【图片】的不动点.如果函数 【图片】,有且仅有两个不动点-1,1,且 【图片】,...
参考答案:
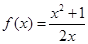
|
参考解析:
由题意知
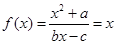 的两个根为-1,1.即
的两个根为-1,1.即
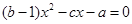 的两个根为-1,1.所以
的两个根为-1,1.所以
 ,又因为
,又因为
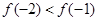 ,所以
,所以
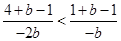 ,所以
,所以
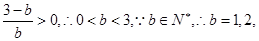
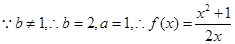 .
.
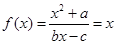 的两个根为-1,1.即
的两个根为-1,1.即
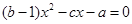 的两个根为-1,1.所以
的两个根为-1,1.所以
 ,又因为
,又因为
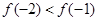 ,所以
,所以
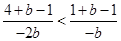 ,所以
,所以
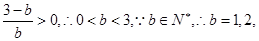
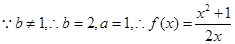 .
.
【简答题】

[4/2000]设函数 【图片】, 【图片】的零点分别为 【图片】,则( ) A. 【图片】B.0< 【图片】<1C.1< 【图片】<2D. ...
参考答案:
|
B
|
参考解析:
由题意知
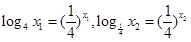 ,画出函数
,画出函数
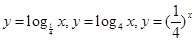 的图像可看出
的图像可看出
 ,则
,则
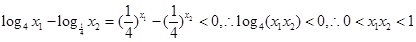 .
.
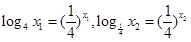 ,画出函数
,画出函数
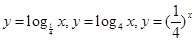 的图像可看出
的图像可看出
 ,则
,则
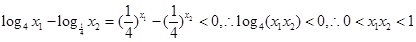 .
.
【简答题】

[5/2000]已知函数 【图片】, 设 【图片】的最大值、最小值分别为 【图片】,若 【图片】, 则正整数 【图片】的取值个数是( ...
参考答案:
|
B
|
参考解析:
本题考查函数值域、基本不等解不等式等知识
思路分析:有根号的先去根号应用平方法,考虑两个式子的平方和为常数可用均值不等式做;另外本题还可考虑用构造二次函数,用函数在闭区间上单调性来做
解:方法一:设 则
则

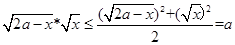 而
而
 所以
所以
 所以
所以
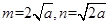 由
由
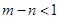 得
得
 所以符合条件的正整数有2个。
所以符合条件的正整数有2个。
方法二:平方之后构造二次函数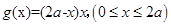
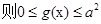 ,同样可以求出
,同样可以求出
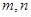
点评:本题以函数值域为载体考查不等式的知识,属于综合题
思路分析:有根号的先去根号应用平方法,考虑两个式子的平方和为常数可用均值不等式做;另外本题还可考虑用构造二次函数,用函数在闭区间上单调性来做
解:方法一:设
 则
则

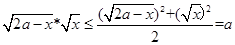 而
而
 所以
所以
 所以
所以
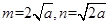 由
由
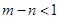 得
得
 所以符合条件的正整数有2个。
所以符合条件的正整数有2个。
方法二:平方之后构造二次函数
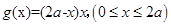
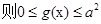 ,同样可以求出
,同样可以求出
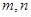
点评:本题以函数值域为载体考查不等式的知识,属于综合题
【简答题】

[6/2000](本小题满分12分) 已知 【图片】,设P:函数 【图片】在R上单调递减,Q:不等式 【图片】的解集为R 如果P和Q有且仅有一个正确,求 【图片】&n...
参考答案:

|
参考解析:
函数
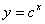 在R上单调递减
在R上单调递减
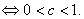 …………
…………
 ………………………2’
………………………2’
不等式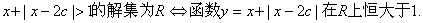
 …………………12’
…………………12’
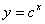 在R上单调递减
在R上单调递减
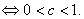 …………
…………
 ………………………2’
………………………2’
不等式
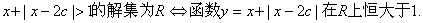
 …………………12’
…………………12’
【简答题】

[7/2000]已知a,b为常数,若 【图片】则 【图片】 .
参考答案:
|
2
|
参考解析:
无
【简答题】

[8/2000]某商场中秋前30天月饼销售总量 f( t)与时间 t(0< t≤30)的关系大致满足 f( t)= t2+10 t+16,则该商场前 t天平均售...
参考答案:
|
A
|
参考解析:
无
【简答题】

[9/2000]设函数 【图片】为奇函数,则 【图片】 &n...
参考答案:
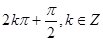
|
参考解析:
因为
 为奇函数,所以
为奇函数,所以
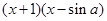 为偶函数,
为偶函数,
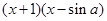 =
=
 ,整理得,sina=1,所以
,整理得,sina=1,所以

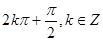 。
。
点评:基础题,利用奇函数定义,确定a的方程。
【简答题】

[10/2000]函数 【图片】的零点为 A. 【图片】B. 【图片】C. 【图片】D. 【图片】
参考答案:
|
D
|
参考解析:
本试题主要是考查了函数零点的概念的运用。
因为求解函数的零点,就是求解方程f(x)=0的解,而函数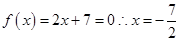 的零点
的零点
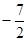 ,选D.
,选D.
解决该试题的关键是令f(x)=0,方程的解即为所求。
因为求解函数的零点,就是求解方程f(x)=0的解,而函数
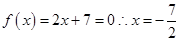 的零点
的零点
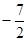 ,选D.
,选D.
解决该试题的关键是令f(x)=0,方程的解即为所求。

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





