
创建自己的小题库
搜索

数列求和的其他方法(倒序相加,错位相减,裂项相加等)题库
题数
2000
考试分类
高中数学>数列求和的其他方法(倒序相加,错位相减,裂项相加等)
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-数列求和的其他方法(倒序相加,错位相减,裂项相加等)
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]各项都为正数的数列 【图片】,其前 【图片】项的和为 【图片】,且 【图片】,若 【图片】,且数列 【图片】的前 【图片】项的和为 【图片】,则 【图...
参考答案:
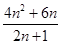
|
参考解析:
本题涉及涉及到数列的前
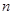 和
和
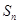 的关系,一般要用到关系式
的关系,一般要用到关系式
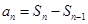 ,由
,由
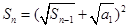 得
得
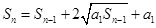 ,所以
,所以
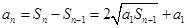 ,于是
,于是
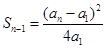 ,
,
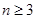 时,
时,
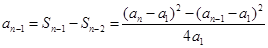 ,化简得:
,化简得:
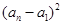
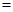
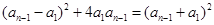 ,即
,即
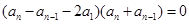 ,由于数列
,由于数列
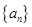 各项为正,故
各项为正,故
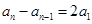 ,又
,又
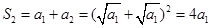 ,即
,即
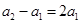 ,因此数列
,因此数列
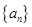 是等差数列,公比为
是等差数列,公比为
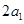 ,所以
,所以
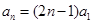 .
.
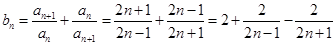 ,
,
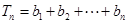
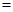
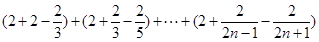
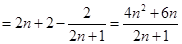 .
.
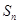 与
与
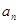 的关系,裂项相消求和.
的关系,裂项相消求和.
【简答题】

[2/2000]数列{an}的前n项和Sn=n(2n-1)an,并且a1= 13,(1)求数列{an}的通项公式.(2)判断前n项和Sn组成的新数列{Sn}的单调性,...
参考答案:
(1)当n≥2时,an=Sn-Sn-1=n(2n-1)an-(n-1)(2n-3)an-1,得
又a1=
(2)因为Sn=n(2n-1)an=
|
参考解析:
an
an-1
【简答题】

[3/2000]已知{an}是等差数列,其中a1=25,a4=16(1)求{an}的通项;(2)求|a1|+|a2|+|a3|+…+|an|的值.
参考答案:
| (1)∵a4=a1+3d ∴d=-3 ∴an=28-3n (2)∵28-3n<0∴n>9
∴数列{an}从第10项开始小于0 ∴|an|=|28-3n|=
当n≤9时,|a1|+|a2|+…+|an|=
当n≥10时,|a1|+|a2|+…+|an|=(|a1|+|a2|+…+|a9|)+(|a10|+|a11|+…+|an|) =
=117+
=
∴|a1|+|a2|+…+|an|=
|
参考解析:
13
【简答题】

[4/2000]对于一个有限数列A:a1,a2,…an,定义A的蔡查罗和(蔡查罗是数学家)为1n(S1+S2+…Sn),其中Sk=a1+a2+…ak(1≤k≤n).若...
参考答案:
| ∵S1=a1,Sn=a1+a2+…+an, ∴S1+S2+S3+…+Sn=na1+(n-1)a2+(n-2)a3+…+2an-1+an, 对于数列a1,a2,…,a99的蔡查罗和为1000 ∴S1+S2+S3+…+S99=99a1+98a2+97a3+…+2a98+a99=1000n=99000, 对于数列2,a1,a2,…,a99 S1+S2+S3+…+S100=200+99a1+98a2+97a3+…+2a98+a99=99200; 所以数列2、a1、a2、a3、…、a99的蔡查罗和为992. 故选B. |
参考解析:
无
【简答题】

[5/2000]已知xi>0(i=1,2,3,…10),且 【图片】xi=1,则T= 【图片】 【图片】的最小值为( )...
参考答案:
| 100 |
参考解析:
无
【简答题】

[6/2000]数列{an}的通项an=n2(cos2nπ3-sin2nπ3),其前n项和为Sn,(1)求Sn;(2)bn= S3nn•4n,求数列{bn}的前n项和...
参考答案:
(1)由于cos2
故S3k=(a1+a2+a3)+(a4+a5+a6)+…+(a3k-2+a3k-1+a3k) =(-
=
S3k-1=S3k-a3k=
S3k-2=S3k-1-a3k-1=
故Sn=
(2)bn=
Tn=
4Tn=
两式相减得3Tn=
故Tn=
|
参考解析:
无
【简答题】

[7/2000]已知数列 【图片】的前 【图片】项和 【图片】(1)求数列的通项公式; (2)求 【图片】...
参考答案:
|
(1)
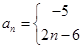
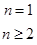
(2)-7 |
参考解析:
(1)
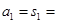 -5
-5
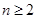 时
时
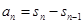 =
=
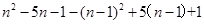
= 2n-6
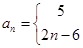
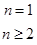
(2)根据题意,由于数列的前3项为非负数,则可知从第4项开始为正数,引起可知数列有最小值,当n=3,n=2时数列的前n项和达到最小,且为(-5)+(-2)+0=-7,因此答案为-7.
点评:主要是考查了等差数列的通项公式与前n项和的关系式的运用,属于基础题。
【简答题】

[8/2000]已知数列{an}满足对任意的n∈N+,都有an>0,且a13+a23+…+an3=(a1+a2+…+an)2.(1)求数列{an}的通项公式an;(2...
参考答案:
| (1)∵a13+a23+…+an3=(a1+a2+…+an)2,① 则有a13+a23+…+an3+an+13=(a1+a2+…+an+an+1)2,② ②-①,得an+13=(a1+a2+…+an+an+1)2-(a1+a2+…+an)2, ∵an>0, ∴an+12=2(a1+a2+…+an)+an+1,③ 同样有an2=2(a1+a2+…+an-1)+an(n≥2),④ ③-④,得an+12-an2=an+1+an. ∴an+1-an=1,又a2-a1=1,即当n≥1时都有an+1-an=1, ∴数列{an}是首项为1,公差为1的等差数列, ∴an=n. (2)由(1)知an=n,则
∴Sn=
=
=
=
∵Sn+1-Sn=
∴数列{Sn}单调递增, ∴(Sn)min=S1=
要使不等式Sn>
∵1-a>0, ∴0<a<1. ∴1-a>a,即0<a<
|
参考解析:
1
anan+2
【简答题】

[9/2000]各项均为正数的数列{an}中,前n项和Sn=( an+12)2.(1)求数列{an}的通项公式;(2)若1a1a2+ 1a2a3+…+ 1anan+1...
参考答案:
(1)∵Sn=(
∴Sn-1=(
两式相减得an=(
整理得(an+an-1)(an-an-1-2)=0, ∵数列{an}的各项均为正数, ∴an-an-1=2,n≥2,∴{an}是公差为2的等差数列,…(4分) 又S1=(
(2)由题意得k>(
∵
∴
=
(3)对任意m∈N+,2m<2n-1<22m,则2m-1+
而n∈N*,由题意可知bm=22m-1-2m-1,…(12分) 于是Sm=b1+b2+…+bm=21+23+…+22m-1-(20+21+…+2m-1) =
即Sm=
|
参考解析:
an+12
【简答题】

[10/2000]设数列{an}的通项an=(-1)n-1•n,前n项和为Sn,则S2010=( ) A.-2010B.-1005C.2010D.1005
参考答案:
| S2010=1+(-2)+3+(-4)+…+2009+(-2010) =[1+(-2)]+[3+(-4)]+…+[2009+(-2010)] =(-1)•
故选B. |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





