在软件应用领域，直接获取（购买）计算机软件常常比自行开发的成本要低得多。软件工程管理者面临着做出自行开发还是购买的决策问题，而且由于存在多种可选的获取方案使得决策更加复杂。这些决策包括：从头开始构造系统；复用已有的"具有部分经验"的构件来构造系统；购买现在的开发软件，并进行修改已满足当前项目的需要；将软件开发承包给外面的开发商。
可以采用决策树分析来帮助管理者进行决策，题目给的图中路径上的数字是出现该情况的概率，树叶金额是出现该情况的成本，成本的期望值=∑（路径概率）×（估算的路径成本），其中i是决策树的某条路径。经过计算可知，采用购买方式预期方式预期成本最低，因此管理者选择建设方式的最佳决策是购买现成的软件产品。

首先，我们直接从来考虑问题。可以根据试题的限制条件：“每个博士生每天只能参加一门课程考试，在这3天内考完全部选修课”，来进行判断各选项是否满足。如果按照A选项，第2天考BD，则因为B1同时选修了这2门课程，将违反“每个博士生每天只能参加一门课程考试”的约束。如果按照B选项，第1天考AC，则因为B2同时选修了这2门课程，将违反“每个博士生每天只能参加一门课程考试”的约束。如果按照c选项，第1天考AF，则因为B3同时选修了这2门课程，将违反“每个博士生每天只能参加一门课程考试”的约束。因此，只有选项D符合要求。下面再介绍另外一种解法（图示法）。将6门课程作为6个结点画出，如图18-14所示。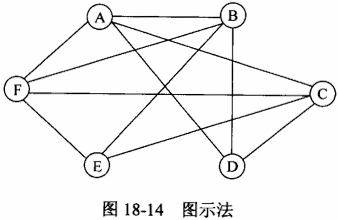我们可以在两个课程结点之间画连线表示他们不可以在同一天安排考试，那么，每个博士生的各门选修课程之间都应画出连线。例如，B1博士生选修了A、B、D三门课程，则ABD之间都应有连线，表示这三门课中的任何二门都不能安排在同一天。从图18-14可以看出，能够安排在同一天考试的课程（结点之间没有连线）有AE、BC、DE、DF。因此，课程A必须与课程E安排在同一天。课程B必须与课程C安排在同一天，余下的课程D只能与课程F安排在同一天。

这是一道求图的最小生成树问题，我们使用克鲁斯卡尔算法来解答，如图9-13所示。到了第5步，就有了多种选择，既可以选择AF，也可以选择BF，因为其路程都是300。我们给出的第6步是选择AF的结果。还有一种结果，就是在第4步时，不是选择AB，而是选择AF或者BF，则结果如图9-14所示。从第6步的结果可以计算出，至少要改造的公路长度为200×2+300×3=1300千米。

设共销售了n套，则总成本=固定成本+每套产品的可变成本×n=160000+2n。销售总收入=单价×n=10n。盈亏平衡时，总成本=销售总收入，所以，160000+2n=10n，从而，n=20000（套）。当销售量低于2万套时，会有亏损；当销售量超过2万套时就会有盈利。

该题考查最小生成树相关知识。解题时，可以采用克鲁斯卡尔算法，从图中，按边权值从小到大顺序来选择边，当选取的边会形成环路时，放弃该边的选择。选足n-1条边时（n为图中的节点数），即为解。依据该原则，得到图9-19，加粗线组成最小生成树。所以电话线总长为：1+2+3+4+4=14。

这是一个简单的博弈问题，可以表示为图18-15所示的得益矩阵。由图18-15可以看出，假设B网站采用高价策略，那么A网站采用高价策略得1000万元，采用低价策略得1500万元。因此，A网站应该采用低价策略。如果B网站采用低价策略，那么A网站采用高价策略得200万元，采用低价策略得700万元，因此A网站也应该采用低价策略。采用同样的方法，也可分析B网站的情况，也就是说，不管A网站采取什么样的策略，B网站都应该选择低价策略。因此，这个博弈的最终结果一定是两个网站都采用低价策略，各得到700万元的利润。这个博弈是一个非合作博弈问题，且两博弈方都肯定对方会按照个体行为理性原则决策，因此虽然双方采用低价策略的均衡对双方都不是理想的结果，但因为两博弈方都无法信任对方，都必须防备对方利用自己的信任（如果有的话）谋取利益，所以双方都会坚持采用低价，各自得到700万元的利润，各得1000万元利润的结果是无法实现的。即使两个网站都完全清楚上述利害关系，也无法改变这种结局。

从实际问题中观察或测量得到的原始数据，通常是不太精确的，也难以完整。需要透过现象看本质，去伪存真，建立比较合理的模型，并求解。建模的过程通常是个渐进的过程。
首先，要根据原始数据初步判断应架构什么样的模型。例如，将一批二维数据画在平面坐标系内，观察它们的分布趋势，初步判断采用什么样的曲线进行拟合比较合适。写出大致的曲线函数表达式，其中必然带有待定的参数。
然后，通过原始数据来估计模型中的参数。算出了参数后，初步的模型就已经建立。但是，该模型是否符合实际，还需要用原始数据来检验。如果发现有些偏差，则需要调整模型或调整参数。一般的建模过程往往要反复多次经历上述过程，逐步优化得到比较合理、适用的模型，然后再选用适当的数值方法进行求解。

这是一道求图的最小生成树问题，我们使用克鲁斯卡尔算法来解答，如图9-13所示。到了第5步，就有了多种选择，既可以选择AF，也可以选择BF，因为其路程都是300。我们给出的第6步是选择AF的结果。还有一种结果，就是在第4步时，不是选择AB，而是选择AF或者BF，则结果如图9-14所示。从第6步的结果可以计算出，至少要改造的公路长度为200×2+300×3=1300千米。

本题考查决策树的使用，利用决策树来进行决策的方法属于风险型决策，我们只要直接计算出各分支的预期收益值，然后选择其中一个最大的值就可以了。
设备供应商1的预期收益值：100000×60%+（-30000）×40%=60000-12000=48000。
设备供应商2的预期收益值：50000×90%+（-10000）×10%=45000-1000=44000。
设备供应商3的预期收益值：10000×99%+（-1000）×1%=9900-10=9890。
设备供应商4的预期收益值：20000×80%+（-10000）×20%=16000-2000=14000。
设备供应商1的预期收益值最大，因此应该选择设备供应商1。