
创建自己的小题库
搜索

绝对值不等式题库
题数
1118
考试分类
高中数学>绝对值不等式
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-绝对值不等式
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1118]已知函数 【图片】. (1)若不等式 【图片】的解集为 【图片】,求实数a的值;(5分) (2)在(1)的条件下,若存在实数 【图片】使 【图片】成立...
参考答案:
|
(1)
 ;(2) ;(2)
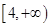 . .
|
参考解析:
本题考查绝对值不等式的解法和存在问题的求法等基础知识,考查学生运用函数零点分类讨论的解题思想和转化思想.第一问,先解绝对值不等式
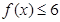 ,得到x的取值范围,由已知条件可知解出的x的取值范围与
,得到x的取值范围,由已知条件可知解出的x的取值范围与
 完全相同,列出等式,解出a;第二问,在第一问
完全相同,列出等式,解出a;第二问,在第一问
 的基础上,
的基础上,
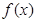 的解析式确定,若存在n使
的解析式确定,若存在n使
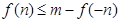 成立,则
成立,则
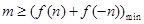 ,构造新的函数
,构造新的函数
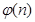 ,去掉绝对值使之化为分段函数,求出最小值代入上式即可.
,去掉绝对值使之化为分段函数,求出最小值代入上式即可.
(1)由
 得
得
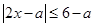 ,∴
,∴
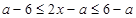 ,即
,即
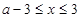 ,
,
∴
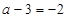 ,∴
,∴
 . 5分
. 5分
(2)由(1)知
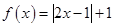 ,令
,令
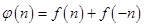 ,
,
则,
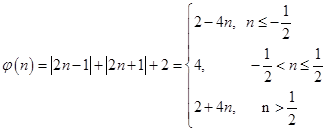
∴
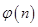 的最小值为4,故实数
的最小值为4,故实数
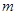 的取值范围是
的取值范围是
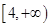 . 10分
. 10分
【简答题】

[2/1118]附加题选做题D.(选修4-5:不等式选讲)设函数f(x)=|x-1|+|x+1|,若不等式|a+b|-|2a-b|≤|a|•f(x)对任意a,b∈R且...
参考答案:
由f(x)≥
而
∴f(x)≥3,即|x-1|+|x+1|≥3, 解得x≤-
所以x的范围为{x|x≤-
|
参考解析:
无
【简答题】

[3/1118]集合A={x∈R||x-2|≤5}中的最小整数为______.
参考答案:
| ∵A={x∈R||x-2|≤5}, ∴由|x-2|≤5得, -5≤x-2≤5, ∴-3≤x≤7, ∴集合A={x∈R||x-2|≤5}中的最小整数为-3. 故答案为-3. |
参考解析:
无
【简答题】

[4/1118]下列四个命题中正确的是 A.若 【图片】,则 【图片】B.若 【图片】,则 【图片】C.若实数 【图片】满足 【图片】,则 【图片】D.若实数 【图片...
参考答案:
|
选C
|
参考解析:
。考查绝对值不等式
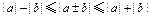 ,主要是其中等号成立的条件。可通过平方进行等价转化。
,主要是其中等号成立的条件。可通过平方进行等价转化。
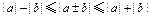 ,主要是其中等号成立的条件。可通过平方进行等价转化。
,主要是其中等号成立的条件。可通过平方进行等价转化。
【简答题】

[5/1118]设函数f(x)=|x-1|+|x-a|。(1)若a=-1,解不等式f(x)≥3;(2)如果 【图片】x∈R,f(x)≥2,求a的取值范围。
参考答案:
|
解:(1)当a=-1时,f(x)=|x-1|+|x+1| |
参考解析:
无
【简答题】

[6/1118](不等式选讲)如果关于x的不等式|x+1|+|x﹣3|<a的解集不是空集,则实数a的取值范围是( )
参考答案:
| a>4 |
参考解析:
无
【简答题】

[7/1118]不等式 【图片】的解集为 &n...
参考答案:
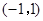
|
参考解析:
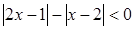 即
即
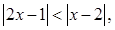 两边平方得,
两边平方得,
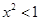 ,
,
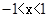 ,
,
所以,不等式
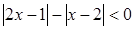 的解集为
的解集为
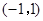 .
.
【简答题】

[8/1118](不等式选做题) 若关于x的不等式|x|+|x-1|≤a有解,则实数a的取值范围是______.
参考答案:
| |x|+|x-1|表示数轴上的x对应点到0和1对应点的距离之和,其最小值为1,故当a≥1时,关于x的不等式|x|+|x-1|≤a有解, 故实数a的取值范围为[1,+∞), 故答案为[1,+∞). |
参考解析:
无
【简答题】

[9/1118]若存在实数x满足|x-3|+|x-m|<5,则实数m的取值范围为( )。
参考答案:
| -2<m<8 |
参考解析:
无
【简答题】

[10/1118](本题10分)已知函数 【图片】(1)解不等式 【图片】; (2)若对 【图片】,恒有 【图片】成立,求 【图片】的取值范围.
参考答案:
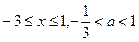
|
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫 ;
; 的解集为
的解集为
 。
。 ,f(x)的最小值为1-a;
,f(x)的最小值为1-a; ,f(x)的最小值为a-1
,f(x)的最小值为a-1 ,f(x)≥2的充要条件是|a-1|≥2
,f(x)≥2的充要条件是|a-1|≥2





