D

C

（1），由线面平行的判定定理的条件是：直线m在平面外，而本题中没有此条件，假命题； （2），由线面垂直的性质定理知：垂直于同一直线的两平面平行，真命题； （3），由线面垂直的判定定理，直线n必须垂直于α内的两条相交直线，本题中没有此条件，假命题； （4），由线面垂直的定义知：若m⊥α，则m垂直于α内所有直线，而n⊂α，则m⊥n，真命题． 故答案为：（2）（4）

连接AC，BD，交点为F，连接EF ∵在△BDD1中，E，F为DD1，BD的中点 故EF∥BD1， ∵EF⊂平面ACE，BD1⊄平面ACE， ∴BD1∥平面ACE， 故选B

由于垂直于同一条直线的两条直线可能相交、平行、异面，故①不对； 垂直于同一个平面的两个平面可能相交也可能平行，故②不对； 与同一平面所成角相等的两条直线的位置关系可以是相交、平行与异面，故③不对； 由三垂线定理知，平面中与直线在面内的射影垂直的直线都与此直线垂直，故④对． 综上，④是真命题 故选D

若直线m、n都平行于平面α，则m、n一定不是相交直线，a，b在与平面α平行的平面β内可以相交，故A错误． B已知平面a、β互相垂直，且直线m、n也互相垂直，若m⊥α，则n⊥β，n与β相交或平行，B错误． C直线m、n在平面α内的射影分别是一个点和一条直线，且m⊥n，则n⊂α或n∥α，正确． D直线m、n是异面直线，若m∥α，则n必与α相交，n可以平行平面α，故错误． 故选C．

（1）垂直于同一平面的两个平面可能互相平行，也可能相交，如教室的东西墙面均与地面垂直，东西墙面相互平行；教室中的西、北墙面均与地面垂直，但西墙面与北墙面相交，故不正确； （2）如果投影面与两条异面直线的公垂线平行，且两条异面直线与投影面均不垂直，此时两条异面直线的投影为两条平行线，故不正确； （3）两个不重合的平面α与β，若α内有不共线的三个点到β的距离相等，则α∥β或α、β相交，故不正确； （4）不重合的两直线a，b和平面α，若a∥b，b⊂α，则a∥α或a⊂α，故不正确． 故选：A．

解：（I）因为PD⊥平面ABCD，BC平面ABCD
所以PD⊥BC
由∠BCD =90°，得BC⊥DC
又PD∩DC =D，PD 平面PCD， DC 平面PCD
所以BC⊥平面PCD
因为PC 平面PCD
所以PC⊥BC；
（Ⅱ）连结AC，设点A到平面PBC的距离为h
因为AB∥DC，∠BCD =90°
所以∠ABC=90°
从而由AB=2，BC=1，得△ABC的面积S _△ABC=1
由PD⊥平面ABCD及PD=1，得三棱锥P-ABC的体积
因为PD⊥平面ABCD，DC 平面ABCD
所以PD⊥DC
又
所以
由
得△ABC的面积
由
得
因此点A到平面PBC的距离为 。

解：（Ⅰ）连接A1C，与AC1交于O点，连接OD． ∵△A1BC中，O、D分别为AC1和BC的中点， ∴ODA1B． 又∵OD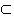平面AC1D，A1B平面AC1D， ∴A1B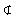平面AC1D．                     （Ⅱ）证明：在直三棱柱ABC﹣A1B1C1中， ∵BB1⊥平面ABC，AD平面ABC， ∴B1B⊥AD． ∵△ABC中，AB=AC，D为BC中点， ∴AD⊥BC． 又∵BC∩B1B=B，BC、B1B平面B1BCC1 ∴AD⊥平面B1BCC1． ∵CE平面B1BCC1，∴AD⊥CE．     ∵四边形B1BCC1为正方形，D，E分别为BC、BB1的中点， ∴Rt△CBE≌Rt△C1CD，可得∠CC1D=∠BCE． ∴∠BCE+∠C1DC=∠CC1D+∠C1DC=90°，可得C1D⊥CE． ∵AD∩C1D=D，AD、C1D平面AC1D ∴CE⊥平面AC1D． 又∵CE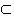平面A1CE， ∴平面A1CE⊥平面AC1D．

C