创建自己的小题库
搜索
复数的四则运算题库
题数
2000
考试分类
高中数学>复数的四则运算
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-复数的四则运算
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/2000]8+6i的平方根是__________.
参考答案：
|
2+3i
|
参考解析：
本题考查复数的平方运算及复数相等的概念.
解法一: 设8+6i的平方根是 x+ yi( x、 y∈R)，则
( x+ yi) 2=8+6i，即 x 2－ y 2+2 xyi=8+6i.
由复数相等，得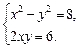
∴
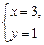或
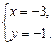
解法二: ∵8+6i=9+6i+i 2=(3+i) 2，∴8+6i的平方根是±(3+i).
解法一: 设8+6i的平方根是 x+ yi( x、 y∈R)，则
( x+ yi) 2=8+6i，即 x 2－ y 2+2 xyi=8+6i.
由复数相等，得
∴
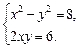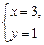或
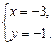
解法二: ∵8+6i=9+6i+i 2=(3+i) 2，∴8+6i的平方根是±(3+i).
【简答题】
[2/2000]已知复数z满足 【图片】，则z=（ ）。
参考答案：
| 3+i |
参考解析：
无
【简答题】
[3/2000]已知z7=1（z∈C且z≠1）．（1）证明1+z+z2+z3+z4+z5+z6=0；（2）设z的辐角为α，求cosα+cos2α+cos4α的值．
参考答案：
| （1）由z（1+z+z2+z3+z4+z5+z6） =z+z2+z3+z4+z5+z6+z7 =1+z+z2+z3+z4+z5+z6， 得（z-1）（1+z+z2+z3+z4+z5+z6）=0．（4分） 因为z≠1，z-1≠0， 所以1+z+z2+z3+z4+z5+z6=0．（6分） （2）因为z7=1．可知|z|=1， 所以z•
由（Ⅰ）知z+z2+z4+z3+z5+z6=-1， 即z+z2+z4+
所以z+z2+z4的实部为-
而z的辐角为α时，复数z+z2+z4的实部为cosα+cos2α+cos4α， 所以cosα+cos2α+cos4α=-
|
参考解析：
.z
【简答题】
[4/2000]设实部为正数的复数z，满足|z|= 10，且复数（1+2i）z在复平面上对应的点在第一、三象限的角平分线，求复数z．
参考答案：
| 设z=a+bi，a，b∈R，a＞0， 由题意：a2+b2=10① （1+2i）z=（1+2i）（a+bi）=a-2b+（2a+b）i， 得a-2b=2a+b② ①②联立，解得a=3，b=-1 得z=3-i． |
参考解析：
无
【简答题】
[5/2000]复数1-3ii3 的共轭复数是（ ） A．-3+iB．-3-iC．3+iD．3-i
参考答案：
所以复数的共轭复数是3-i． 故选D． |
参考解析：
1-3i
i3
【简答题】
[6/2000]复数z=1-i2+i在复平面内所表示的点在（ ） A．第一象限B．第二象限C．第三象限D．第四象限
参考答案：
z=
则复数z对应的点为（
所以复数z对应的点在第四象限， 故选D． |
参考解析：
无
【简答题】
[7/2000]已知复数 【图片】满足 【图片】．求 【图片】 &nbs...
参考答案：
|
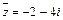
参考解析：
无
【简答题】
[8/2000]复数 【图片】= [ ] A．﹣3﹣4iB．﹣3+4iC．3﹣4iD．3+4i
参考答案：
| A |
参考解析：
无
【简答题】
[9/2000]复数 【图片】的值是 （ &nb...
参考答案：
|
B
|
参考解析：
无
【简答题】
[10/2000]设z=1-i（i为虚数单位），.z是z的共轭复数，则z .z+ 2z的值为（ ） A．-1-iB．1+iC．3-iD．3+i
参考答案：
∵z
故选 D． |
参考解析：
无
