创建自己的小题库
搜索
线段的定比分点题库
题数
79
考试分类
高中数学>线段的定比分点
售价
¥10
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-线段的定比分点
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/79]若过两点 【图片】的直线与 【图片】轴相交于点P，则点P分有向线段 【图片】所成的比 【图片】的值为 ...
参考答案：
|
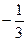
参考解析：
略
【简答题】
[2/79]若点P分 【图片】所成的比例为 【图片】，则A分 【图片】所得的比是（ ） A． 【图片】 B． 【图片】 C．- 【图片】 D．- 【图片】
参考答案：
| C |
参考解析：
无
【简答题】
[3/79]已知 【图片】A、B、C三点共线，A分 【图片】的比为 【图片】，A，B的纵坐标分别为2，5，则点C的纵坐标为 &n...
参考答案：
|
D
|
参考解析：
略
【简答题】
[4/79]已知两点 【图片】，则直线 【图片】与 【图片】轴的交点分有向线段 【图片】的比为 。
参考答案：
|
2
|
参考解析：
无
【简答题】
[5/79]在直角坐标系xOy中，已知点A(0，1)和点B(-3，4)，若点C在∠AOB的平分线上且| 【图片】|=2，则 【图片】=（ &...
参考答案：
 |
参考解析：
无
【简答题】
[6/79]过点M（0，1）作直线，使它被两直线l1：x-3y+10=0，l2：2x+y-8=0所截得的线段恰好被M所平分，求此直线方程。
参考答案：
解：过点M且与x轴垂直的直线是y轴，它和两已知直线的交点分别是 和（0，8），显然不满足中点是点M（0，1）的条件故可设所求直线方程为y=kx+1，与两已知直线l1，l2分别交于A、B两点， 联立方程组  ①  ② 由①解得xA=  ，由②解得xB= ∵点M平分线段AB， ∴xA+xB=2xM，即  解得k=-  ，故所求直线方程为x+4y-4=0。 |
参考解析：
无
【简答题】
[7/79]已知两点P1（2，-1）、P2（0，5），点P在P1P2延长线上，且满足P1P2=-2 PP2，则P点的坐标为______．
参考答案：
| 设分点P（x，y），P1（2，-1）、P2（0，5）， ∴
∵
∴（-2，6）=-2（-x，5-y） -2=-2x，6=2y-10， ∴x=-1，y=8 ∴P（-1，8）． |
参考解析：
无
【简答题】
[8/79]已知向量 【图片】，且 【图片】，则点P的坐标为 [ ] A.（2，-4） B.（ 【图片】）C.（ ...
参考答案：
| C |
参考解析：
无
【简答题】
[9/79]已知两点M（﹣1，﹣6），N（3，0），点P（﹣ 【图片】，y）分有向线段 【图片】的比为λ，则λ，y的值为 [ &...
参考答案：
| C |
参考解析：
无
【简答题】
[10/79]点P分向量 【图片】所成的比为1，则 【图片】分向量 【图片】所成的比为 A．1 B．-1 C． 【图片】 D． 【图片】
参考答案：
| D |
参考解析：
无
