
创建自己的小题库
搜索

空间向量的定义题库
题数
455
考试分类
高中数学>空间向量的定义
售价
¥20
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-空间向量的定义
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/455]已知点P为三棱锥O-ABC的底面ABC所在平面内的一点,且 【图片】则实数k的值为( ) A.- 【图片】 B. 【图片】 C.1 D. 【图片】
参考答案:
| D |
参考解析:
无
【简答题】

[2/455]如图,底面 【图片】是边长为2的菱形,且 【图片】,以 【图片】与 【图片】为底面分别作相同的正三棱锥 【图片】与 【图片】,且 【图片】. 【图片】...
参考答案:
|
(1)证明过程见解析;(2)
 . .
|
参考解析:
(1)作
 面
面
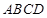 于
于
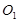 ,作
,作
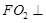 面
面
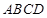 于
于
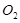 ,易得四边形
,易得四边形
 是平行四边形,所以
是平行四边形,所以
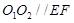 .又
.又
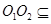 面
面
 ,
,
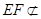 面
面
 ,所以
,所以
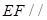 平面
平面
 ;
;
(2)以
 为
为
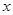 轴的正方向,以
轴的正方向,以
 为
为
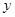 轴的正方向,在平面
轴的正方向,在平面
 中过
中过
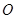 点作面
点作面
 的垂线为
的垂线为
 轴,建立空间直角坐标系求题,利用向量,求出平面
轴,建立空间直角坐标系求题,利用向量,求出平面
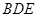 和平面
和平面
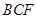 的法向量,则两平面的法向量的夹角即为所求角或为所求角的补角.
的法向量,则两平面的法向量的夹角即为所求角或为所求角的补角.
(1)作
 面
面
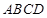 于
于
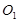 ,作
,作
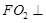 面
面
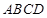 于
于
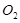 ,因
,因
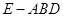 与
与
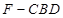 都是正三棱锥, 且
都是正三棱锥, 且
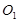 、
、
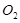 分别为
分别为
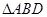 与
与
 的中心,
的中心,

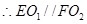 且
且
 .
.
所以四边形
 是平行四边形,所以
是平行四边形,所以
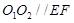 .
.
又
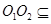 面
面
 ,
,
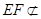 面
面
 ,所以
,所以
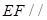 平面
平面

(2)如图,建立空间直角坐标系,
 、
、
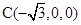 、
、
 、
、
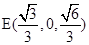 、
、
 .
.
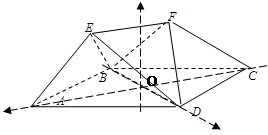
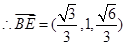 、
、
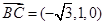 、
、
 、
、
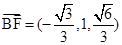 .…7分
.…7分
设
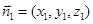 为平面
为平面
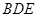 的法向量,
的法向量,
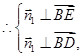
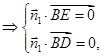
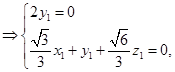
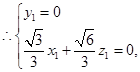

设
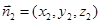 为平面
为平面
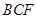 的法向量,
的法向量,

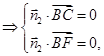
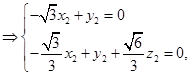
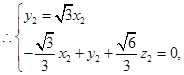

设平面
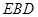 与平面
与平面
 所成锐二面角为
所成锐二面角为
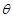 ,
,
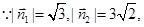

所以,面
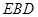 与面
与面
 所成锐二面角的余弦值为
所成锐二面角的余弦值为
 .
.
【简答题】

[3/455](本小题满分12分) 已知斜三棱柱 【图片】, 【图片】, 【图片】, 【图片】在底面 【图片】上的射影恰 为 【图片】的中点 【图片】, 【图片】为...
参考答案:
|
法一:(I)如图,
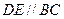 ,因为 ,因为
 ,所以 ,所以
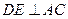 ,又 ,又
 平面 平面
 , ,
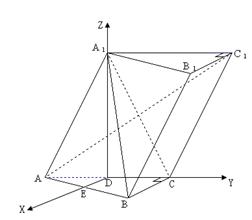
以  为 为
 轴建立空间坐标系,则 轴建立空间坐标系,则
 , ,
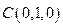 , ,
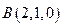 , ,
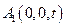 , ,
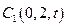 , ,
 , ,
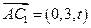 , ,
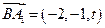 , ,
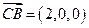 ,由 ,由
 , ,
知  ,又 ,又
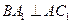 ,从而 ,从而
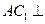 平面 平面
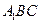 ; ;
(II)由 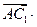
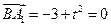 ,得 ,得
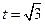 。 。
设平面 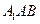 的法向量为 的法向量为
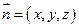 , ,
 , ,
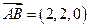 ,所以 ,所以
 ,设 ,设
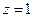 ,则 ,则

再设平面 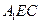 的法向量为 的法向量为
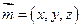 , ,
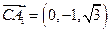 , ,
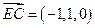
所以 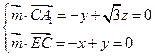 ,设 ,设
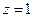 ,则 ,则
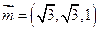
故 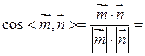
 , 可知二面角 , 可知二面角
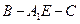 余弦值的大小 余弦值的大小
 . .

法二: (I)如图, 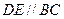 ,因为 ,因为
 , ,
 平面 平面
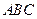 ,所以 ,所以
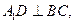 又 又
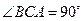 ,所以 ,所以
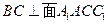 , ,
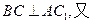
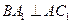 从而 从而
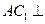 平面 平面
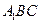 ; ;
(II)由(I)知 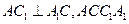 为菱形, 为菱形,
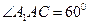
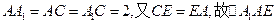 ≌ ≌
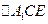 . .
作 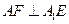 于 于
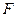 ,连 ,连
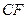 ,则 ,则

故  为二面角 为二面角
 的平面角, 的平面角,
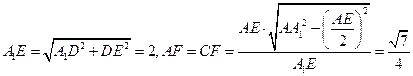
 . .
故二面角 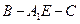 余弦值的大小 余弦值的大小
 . .
|
参考解析:
略
【简答题】

[4/455]已知正方体 ABCD- A1B1C1D1中, E为侧面 BCC1B1的中心.若 【图片】,则 x+ y+ z的值为( ) A.1 B. 【图片】 C...
参考答案:
| C |
参考解析:
无
【简答题】

[5/455]给出下列结论:①若 【图片】 , 【图片】,则 【图片】 ; ②若 【图片】,则 【图片】; ③ 【图片】; ...
参考答案:
|
C
|
参考解析:
①
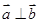 也满足条件; ②若
也满足条件; ②若
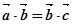 ,则
,则
 ,不能得到
,不能得到
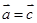 ;
;
③不成立,左边是与
 共线的向量,右边是与
共线的向量,右边是与
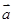 共线的向量; ④正确;⑤正确.
共线的向量; ④正确;⑤正确.
【简答题】

[6/455]设点M是 Z轴上一点,且点M到 A(1,0,2)与点B(1,-3,1)的距离相等,则点M的坐标是( ) A.(-3,-3,0)...
参考答案:
|
B
|
参考解析:
设出M点的坐标,利用点M到A(1,0,2)与点B(1,-3,1)的距离相等,列出方程即可求出M的坐标.解:由题意设M(0,0,z),因为点M到A(1,0,2)与点B(1,-3,1)的距离相等,则可知
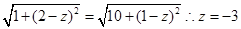 所以M的坐标为(0,0,-3).故选B
所以M的坐标为(0,0,-3).故选B
点评:本题考查空间两点的距离公式的求法,考查计算能力.
【简答题】

[7/455]已知实数x,y,z满足 【图片】,则 【图片】的最小值是( ) A. 【图片】B.3C.6D.9
参考答案:
|
D
|
参考解析:
由已知得,点P(x,y,z)在以M(3,4,0)为球心,2为半径的球面上,
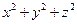 表示原点O与点P的距离的平方,显然当O,P,M共线且P在O与M之间时,|OP|最小.
表示原点O与点P的距离的平方,显然当O,P,M共线且P在O与M之间时,|OP|最小.
此时|OP|=|OM|-2= -2=3.
-2=3.
∴|OP| 2=9.即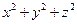 的最小值是9,选D.
的最小值是9,选D.
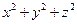 表示原点O与点P的距离的平方,显然当O,P,M共线且P在O与M之间时,|OP|最小.
表示原点O与点P的距离的平方,显然当O,P,M共线且P在O与M之间时,|OP|最小.
此时|OP|=|OM|-2=
 -2=3.
-2=3.
∴|OP| 2=9.即
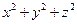 的最小值是9,选D.
的最小值是9,选D.
【简答题】

[8/455]在 【图片】中,已知 【图片】, 【图片】则 【图片】的值为 .
参考答案:
|
±2
|
参考解析:
略
【简答题】

[9/455]给出下列四个命题: ① 因为 【图片】,所以 【图片】; ② 由 【图片】两边同除 【图片】,可得 【图片】; ③ 数列1,4,7,10,…, 【图片...
参考答案:
|
A
|
参考解析:
①复数不能比较大小,所以不正确;②向量不能做普通的代数除法,所以不正确;③,
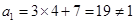 ,所以不正确;④根据演绎揄与类比推理的概念知正确.综上选A.
,所以不正确;④根据演绎揄与类比推理的概念知正确.综上选A.
【简答题】

[10/455]如图,在直三棱柱 【图片】中, AB=1, 【图片】, 【图片】. (Ⅰ)证明: 【图片】; (Ⅱ)求二面角A— 【图片】—B的余弦值。 【图片】
参考答案:
|
(1)证:
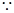 三棱柱 三棱柱
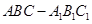 为直三棱柱, 为直三棱柱,
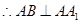 …1分 …1分
在 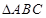 中, 中,
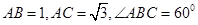 ,由正弦定理 ,由正弦定理
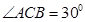 , ,
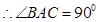
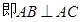 …………3分 …………3分
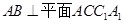 ,又 ,又
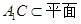
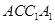
 ……5分 ……5分
(2)解如图,作 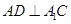 交 交
 于点D点,连结BD, 于点D点,连结BD,
由线面垂直的性质定理知  …………7分 …………7分
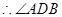 为二面角 为二面角
 的平面角。 ……8分 的平面角。 ……8分
在  …………9分 …………9分
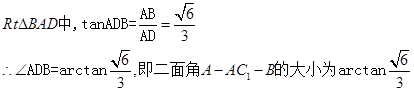
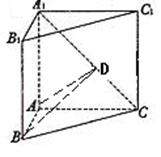
|
参考解析:
略

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





