
创建自己的小题库
搜索

反函数题库
题数
900
考试分类
高中数学>反函数
售价
¥25
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-反函数
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/900]函数f(x)=x2+1(x≤0)的反函数f-1(x)=______.
参考答案:
| 函数f(x)=x2+1(x≤0)可得x2=y-1,y≥1 x=-
可得函数的反函数f-1(x)=-
故答案为:-
|
参考解析:
y-1
【简答题】

[2/900]为研究“原函数图象与其反函数图象的交点是否在直线y=x上”这个课题,我们可以分三步进行研究:(I)首先选取如下函数:y=2x+1,y= 2xx+1,y...
参考答案:
| (II)原函数的图象与反函数的图象的交点不一定在直线y=x上. (III)证明:设(a,b)是f(x)的图象与其反函数的图象的任一点, 由于原函数与反函数的图象关于直线y=x对称, 则(b,a)也是f(x)的图象与反函数的图象的交点, 且b=f(a),a=f(a), 若a>b时,交点显然在y=x上. 若a<b,且f(x)是增函数时,有f(b)<f(a),从而b<a.矛盾; 若b<a,且f(x)是增函数时,有f(a)<f(b),从而a<b.矛盾; 若a<b,且f(x)是减函数时,有f(b)<f(a),从而a<b.此时交点不在y=x上; 若b<a,且f(x)是减函数时,有f(a)<f(b),从而b<a.此时交点不在y=x上. 综上所述,f(x)单调递增,且f(x)的图解与其反函数的图象有交点时,交点在y=x上;f(x)单调递减,且f(x)的图解与其反函数的图象有交点时,交点不在y=x上. |
参考解析:
无
【简答题】

[3/900]记函数y=f(x)的反函数为y=f-1(x).如果函数y=f(x)的图象过点(1,0),那么函数y=f-1(x)+1的图象过点______.
参考答案:
| ∵y=f(x)的图象过点(1,0), ∴其反函数y=f-1(x)必过点(0,1),即f-1(0)=1, ∴y=f-1(x)+1的图象过点(0,2). 故答案为:(0,2). |
参考解析:
无
【简答题】

[4/900]已知函数 【图片】 .(1)用定义证明:函数f(x)在(﹣∞,+∞)内单调递增;(2)记f﹣1(x)为函数f(x)的反函数,求函数m=f﹣1...
参考答案:
|
证明:(1)任取x1<x2,则 |
参考解析:
无
【简答题】

[5/900]设f(x)=x5-5x4+10x3-10x2+5x+1,则f(x)的反函数f-1(x)=______.
参考答案:
| ∵y=x5-5x4+10x3-10x2+5x+1=(x-1)5+2, ∴x=(y-2)
∴f(x)的反函数f-1(x)=
故答案为:
|
参考解析:
无
【简答题】

[6/900]已知函数f(x)= 2x+1x+a(x≠-a,a≠ 12)(1)求f(x)的反函数f-1(x);(2)若f(x)=f-1(x),求a的值.
参考答案:
(1)f(x)=2+
∴反函数f-1(x)=
(2)由f(x)=f-1(x),有2+
即(a+2)(x-2)(x+a)=(a+2)(1-2a) 使上式对x≠2且x≠a都成立,则a=-2 |
参考解析:
1-2ax+a
【简答题】

[7/900]已知 【图片】的反函数为 【图片】,则 【图片】的定义域为( ) A 【图片】 &...
参考答案:
|
D
|
参考解析:
转化为求
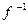 (x)的值域
(x)的值域
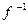 (x)的值域
(x)的值域
【简答题】

[8/900]函数 【图片】的反函数是 [ ] A、 【图片】B、 【图片】 C、 【图片】D、 【图片】
参考答案:
| B |
参考解析:
无
【简答题】

[9/900]已知函数 【图片】存在反函数 【图片】,若函数 【图片】的图像经过点 【图片】,则 【图片】的值是___________.
参考答案:
|
2
|
参考解析:
本题关键是出函数
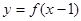 的反函数,由
的反函数,由
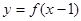 得
得
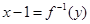 ,
,
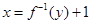 ,即函数
,即函数
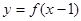 的反函数为
的反函数为
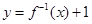 ,那么这个反函数图象一定过点
,那么这个反函数图象一定过点
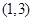 ,所以
,所以
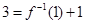 ,
,
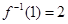 .
.
【简答题】

[10/900]已知函数 【图片】,则 【图片】A. 【图片】B. 【图片】C. 【图片】D. 【图片】
参考答案:
|
A
|
参考解析:
本题考查反函数的概念,互为反函数的关系.
若函数 的反函数为
的反函数为
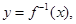 则
则

因为由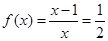 解得
解得
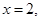 所以
所以
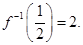 故选A
故选A
若函数
 的反函数为
的反函数为
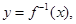 则
则

因为由
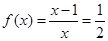 解得
解得
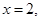 所以
所以
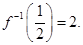 故选A
故选A

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, .
. 





