创建自己的小题库
搜索
函数的单调性与导数的关系题库
题数
2000
考试分类
高中数学>函数的单调性与导数的关系
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-函数的单调性与导数的关系
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/2000]以初速度40m/s向上抛一物体，ts时刻的位移 【图片】 ，则此物体达到最高 时的高度为（ ...
参考答案：
|
A
|
参考解析：
分析：由题意，令v=40-10t
2=0解得速度为0时的时刻，此时物体达到最高高度，再速度的积分求出路程，即可选出正确答案
解答：解：由v=40-10t 2=0，得物体达到最高时t=2，
此时物体距地面的高度是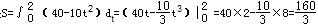
故答案为A
解答：解：由v=40-10t 2=0，得物体达到最高时t=2，
此时物体距地面的高度是
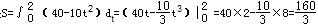故答案为A
【简答题】
[2/2000]已知向量i=（1，0），j=（0，1），函数f（x）=ax3+bx2+c（a≠0）的图象在y轴上的截距为1，在x=2处切线的方向向量为（a-c）i-1...
参考答案：
（1）f（0）=1，c=1∴f′（x）=3ax2+2bx；
（2）f′（x）=12x2-12x=12x（x-1）＞0，∴f（x）的单调递增区间为（1，+∞）和（-∞，0）． （3）由（2）知，f（x）的单调递增区间为（1，+∞）和（-∞，0），由f′（x）＜0得单调递减区间为（0，1），∴x=0时，函数取极大值f（0）=1，x=1时，函数取极小值（1）=-1 |
参考解析：
| f′(1)=0 | ||
f′(2)=
|
【简答题】
[3/2000]设函数f（x）=13x3-12x2+2x，g（x）=12ax2-（a-2）x，（I）对于任意实数x∈[-1，2]，f′（x）≤m恒成立，求m的最小值；...
参考答案：
（I）f′（x）=x2-x+2≤m，对称轴x=
（II）令h（x）=f（x）-g（x）=
依题意得2x2-3（a+1）x+6a=0有两个大于-1且不等于0的根， ∴
|
参考解析：
12
【简答题】
[4/2000]设函数f（x）=x2+bln（x+1），其中b≠0．（1）若b=-12，求f（x）在[1，3]的最小值；（2）如果f（x）在定义域内既有极大值又有极小...
参考答案：
| （1）由题意知，f（x）的定义域为（1，+∞） b=-12时，由f′(x)=
当x∈[1，2）时f′（x）＜0，当x∈（2，3]时，f′（x）＞0， 所以当x∈[1，2）时，f（x）单调递减；当x∈（2，3]时，f（x）单调递增， 所以f（x）min=f（2）=4-12ln3 （2）由题意f′(x)=
即2x2+2x+b=0在（-1，+∞）有两个不等实根， 设g（x）=2x2+2x+b，则
|
参考解析：
2
x2+2x-12x+1
【简答题】
[5/2000]函数f（x）=sin2x在（0，π）上的递减区间是 ______．
参考答案：
∵f(x)=
y=cos2x在(0，
得f（x）在(0，
故答案为（
|
参考解析：
12
【简答题】
[6/2000]设a∈R，函数f（x）=ax3-2x2-4ax，（1）若x=2是函数y=f（x）的极值点，求a的值；（2）在（1）的条件下，求函数f（x）在区间[-1...
参考答案：
| f′（x）=3ax2-4x-4a． （1）∵x=2是函数y=f（x）的极值点，∴f′（2）=12a-8-4a=0． 解得a=1． 经验证a=1符合函数取得极值的条件； （2）∵f′（x）=3x2-4x-4=（3x+2）（x-2）， 令f′（x）=0，解得x=-
又f（-1）=1，f(-
因此函数f（x）的最大值是55，最小值是-8． （3）∵f′（x）=3ax2-4x-4a，要使函数f（x）在R上单调递增，则f′（x）≥0在R上恒成立， 则a必须满足△=16+16a×3a≤0，因此不存在a满足条件． |
参考解析：
23
【简答题】
[7/2000]函数 f( x)= x3＋ ax－2在区间(1,＋∞)内是增函数,则实数 a的取值范围是 A．［3,＋∞ 【图片】B．［－3,＋∞ 【图片】C．(－3...
参考答案：
|
B
|
参考解析：
本题考查函数的单调性与导数的关系.
由 f′( x)=3 x 2＋ a,
令 f′( x)=3 x 2＋ a＞0,得 x 2＞－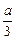
.
解得 x＜－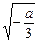
或
x＞
(
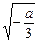a＜0).
∵函数 f( x)在(1,＋∞)上为增函数,
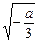∴≤1,即
a≥－3.
由 f′( x)=3 x 2＋ a,
令 f′( x)=3 x 2＋ a＞0,得 x 2＞－
.
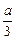解得 x＜－
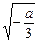或
x＞
(
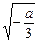a＜0).
∵函数 f( x)在(1,＋∞)上为增函数,
∴
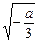≤1,即
a≥－3.
【简答题】
[8/2000]函数f（x）=ax3+bx2+cx+3-a，（a，b，c∈R，且a≠0）当x=-1时，f（x）取得极大值2（1）用关于a的代数式分别表示b与c．（2）...
参考答案：
（1）f′（x）=3ax2+2bx+c∴
（2）由（1）得f′(x)=3ax2+2(a+1)x+2-a=3a(x+1)(x-
令f′（x）=0解得x1=-1，x2=
∴要使f（x）极大值为f（-1）=2，则
∴a＞
|
参考解析：
| f(-1)=2 |
| f′(-1)=0 |
【简答题】
[9/2000]已知函数f（x）=（ax+1）a-x，a＞0且a≠1，讨论f（x）的单调性，并求出极值点x0．
参考答案：
| f'（x）=aa-x-a-xlna（ax+1） 令f'（x）=0，解得x=
当0＜a＜1时，令f'（x）＜0，解得x∈(-∞，
令f'（x）＞0，解得x∈(
∴f（x）在(-∞，
当a＞1时，令f'（x）＞0，解得x∈(-∞，
令f'（x）＜0，解得x∈(
f（x）在上(
极值点x0=
|
参考解析：
a-lnaalna
【简答题】
[10/2000]函数y＝xcos x－sin x在下面哪个区间内是增函数( ) A． 【图片】B．(π，2π)C． 【图片】D．(2π，3π)
参考答案：
|
B
|
参考解析：
y‘=cosx-xsinx-cosx=-xsinx
欲使导数为正，只需x与sinx符号总相反，
分析四个选项知，B选项符合条件，
故应选B．
欲使导数为正，只需x与sinx符号总相反，
分析四个选项知，B选项符合条件，
故应选B．
