
创建自己的小题库
搜索

反冲运动题库
题数
63
考试分类
高中物理>反冲运动
售价
¥10
 手机预览
手机预览
收藏
分享
去刷题
简介
高中物理-反冲运动
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/63]人静止于光滑冰面上,现欲前进,下列方法中可行的是( ) A.向后踢腿B.手臂向前甩C.在冰上滚D.脱去外衣向后投掷
参考答案:
|
D
|
参考解析:
欲使物体获得一定的动量,必须有外力作用在该物体上.A、B两种方法属于物体两部分间的作用,不会对物体产生冲量;因冰面是光滑的,故C也不行.
【简答题】

[2/63]倾角为θ、长为L的斜面置于光滑水平面上,如图8-5-2所示.已知斜面质量为M,今有一质量为m的滑块从斜面上端开始下滑,求滑块滑到底端时,斜面后退的位移...
参考答案:
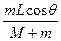
|
参考解析:
在两物体相互作用的过程中,水平方向上动量时时守恒,其速度可取平均速度,本题可取后退方向为正方向,列动量守恒方程:0=M·
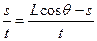 ,即s=
,即s=
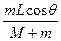 .
.
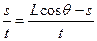 ,即s=
,即s=
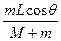 .
.
【简答题】

[3/63]如图13-1所示,物体A从高h的P处沿光滑曲面从静止开始下滑,物体B用长为L的细绳竖直悬挂在O点且刚和平面上Q点接触。已知mA=mB,高h及S(平面部...
参考答案:
小题1:A与B碰后,B必做圆周运动。因此(1)的解为:A与B碰后A停在Q处,B做圆周运动,经一周后,B再次与A相碰,B停在Q处,A向右以 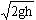 速度做匀速直线运动。 速度做匀速直线运动。
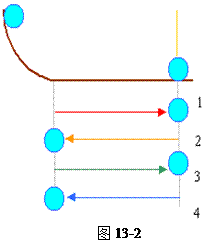
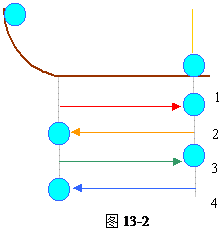
小题2:(2)由上面分析可知,当L=h时,A与B碰后,B只做摆动,因水平面粗糙,所以A在来回运动过程中动能要损失。设碰撞次数为n,由动能定理可得: m Agh-n μm AgS="0" 所以n=h/ μS 讨论:若n为非整数时,相碰次数应凑足整数数目。 如n=1.2,则碰撞次数为两次。 当n为奇数时,相碰次数为(n-1)次。如n=3,则相碰次数为两次,且A球刚到达Q处将碰B而又未碰B; 当n为偶数时,相碰次数就是该偶数的数值,如n=4,则相碰次数为四次。球将停在距B球S处的C点。A球停留位置如图13-2所示 |
参考解析:
当水平部分没有摩擦时,A球下滑到未碰B球前能量守恒,与B碰撞因无能量损失,而且质量相等,由动量守恒和能量守恒可得两球交换速度。A 停在Q处,B碰后可能做摆动,也可能饶 O点在竖直平面内做圆周运动。如果做摆动,则经一段时间,B反向与A相碰,使A又回到原来高度,B停在Q处,以后重复以上过程,如此继续下去,若B做圆周运动,B逆时针以O为圆心转一周后与A相碰,B停在Q处,A向右做匀速运动。由此分析,我们可得本题的解如下:
小题1:(1)A与B碰撞前A的速度:mgh=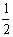 mV
A
2,V
A=
mV
A
2,V
A=
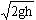
因为m A=m B,碰撞无能量损失,两球交换速度,得:V A’=0,V B’=V A=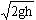
设B球到最高点的速度为Vc,B做圆周运动的临界条件:m Bg=m BV 2/L [1]
又因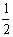 m
BV
B‘
2=
m
BV
B‘
2=
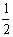 m
BV
2+m
Bg2L [2]
m
BV
2+m
Bg2L [2]
将[1]式及V B’=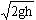 代入[2]式得:L=2h/5
代入[2]式得:L=2h/5
即L≤2h/5时,A、B碰后B才可能做圆周运动。而题意为L=h/4<2h/5,故A与B碰后,B必做圆周运动。因此(1)的解为:A与B碰后A停在Q处,B做圆周运动,经一周后,B再次与A相碰,B停在Q处,A向右以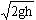 速度做匀速直线运动。
速度做匀速直线运动。
小题2:(2)由上面分析可知,当L=h时,A与B碰后,B只做摆动,因水平面粗糙,所以A在来回运动过程中动能要损失。设碰撞次数为n,由动能定理可得:
m Agh-n μm AgS="0" 所以n=h/ μS
讨论:若n为非整数时,相碰次数应凑足整数数目。
如n=1.2,则碰撞次数为两次。
当n为奇数时,相碰次数为(n-1)次。如n=3,则相碰次数为两次,且A球刚到达Q处将碰B而又未碰B;
当n为偶数时,相碰次数就是该偶数的数值,如n=4,则相碰次数为四次。球将停在距B球S处的C点。A球停留位置如图13-2所示

小题1:(1)A与B碰撞前A的速度:mgh=
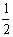 mV
A
2,V
A=
mV
A
2,V
A=
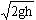
因为m A=m B,碰撞无能量损失,两球交换速度,得:V A’=0,V B’=V A=
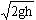
设B球到最高点的速度为Vc,B做圆周运动的临界条件:m Bg=m BV 2/L [1]
又因
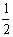 m
BV
B‘
2=
m
BV
B‘
2=
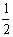 m
BV
2+m
Bg2L [2]
m
BV
2+m
Bg2L [2]
将[1]式及V B’=
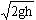 代入[2]式得:L=2h/5
代入[2]式得:L=2h/5
即L≤2h/5时,A、B碰后B才可能做圆周运动。而题意为L=h/4<2h/5,故A与B碰后,B必做圆周运动。因此(1)的解为:A与B碰后A停在Q处,B做圆周运动,经一周后,B再次与A相碰,B停在Q处,A向右以
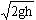 速度做匀速直线运动。
速度做匀速直线运动。
小题2:(2)由上面分析可知,当L=h时,A与B碰后,B只做摆动,因水平面粗糙,所以A在来回运动过程中动能要损失。设碰撞次数为n,由动能定理可得:
m Agh-n μm AgS="0" 所以n=h/ μS
讨论:若n为非整数时,相碰次数应凑足整数数目。
如n=1.2,则碰撞次数为两次。
当n为奇数时,相碰次数为(n-1)次。如n=3,则相碰次数为两次,且A球刚到达Q处将碰B而又未碰B;
当n为偶数时,相碰次数就是该偶数的数值,如n=4,则相碰次数为四次。球将停在距B球S处的C点。A球停留位置如图13-2所示
【简答题】

[4/63]一火箭喷气发动机每次喷出m=200 g的气体,喷出的气体相对地面的速度v=1 000 m/s。设此火箭初始质量M=300 kg,发动机每秒喷气20次,...
参考答案:
| 解:解法一:(归纳法) 以火箭、喷出的气体为研究对象,系统动量守恒 第一次喷出气体后,火箭速度为v1,(M-m)v1-mv=0,所以  第二次喷出气体后,火箭速度为v2,(M-2m)v2-mv=(M-m)v1,得  第三次喷出气体后,火箭速度为v3,(M-3m)v3-mv=(M-2m)v2,所以  以此类推,第n次喷出气体后,火箭速度为vn,有  因为每秒喷气20次,所以1s末火箭速度为:  解法二:(整体法) 以火箭和它在1s内喷出的气体为研究对象,设火箭Is末的速度为v',1s内共喷出质量为20m的气体,以火箭前进的方向为正方向 由动量守恒定律得:(M-20m)v'-20mv=0 解得  |
参考解析:
无
【简答题】

[5/63]对于下列现象,以下判断正确的是( ) A.喷气式飞机能飞出大气层B.每秒钟喷出一定量的气体时,喷气速度越大,飞机受到...
参考答案:
|
BC
|
参考解析:
因喷气式飞机靠的是从进气道吸入气体然后高速喷出而获得强大的“反推”作用力,故不能飞出大气层,所以A错,B对.根据牛顿第一定律知:减小质量,惯性减小,C对.
【简答题】

[6/63]小船相对于地面以速度 v 向东行驶,若在船上以相对地面的相同速率 v 分别水平向 东向西抛出两个质量相等的重物,则小船的速度将( ...
参考答案:
|
C
|
参考解析:
以两重物和船为系统,抛重物的过程系统满足动量守恒定律的条件,即(M+2m)v=mv-mv+Mv′,所以v′=(M+2m)v/M>v,故选C.
【简答题】

[7/63]一质量为6×10 3 kg的火箭从地面竖直向上发射,若火箭喷射燃料气体的速率(相对于火箭)为10 3 m/s,求: (1)每秒钟喷出多少气体才能有克服...
参考答案:
|
(1)60 kg/s (2)180 kg/s
|
参考解析:
这是一个反冲运动的问题,火箭升空是喷出的气体对火箭反作用力的结果,可以根据动量定理先求出火箭对气体的作用力.
(1)以喷出的气体质量为研究对象,设每秒喷出的质量为Δm,火箭对这部分气体的作用力为F,由动量定理有 FΔt=Δmv 0 ①
火箭刚要升空时对地速度为零,此时气体相对火箭的速度也就是气体对地的速度,气体对火箭的反作用力F′=F.对火箭(因忽略气体的重力)F′="Mg " ②
由①②两式解得
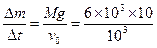 kg/s="60" kg/s
kg/s="60" kg/s
即要获得克服火箭重力的推力,每秒要喷出60 kg的气体.
(2)同第(1)问,以喷出的气体Δm为对象.
FΔt=Δmv 0 ③
而对火箭F-Mg="Ma " ④
由③④两式解得
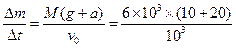 kg/s="180" kg/s.
kg/s="180" kg/s.
(1)以喷出的气体质量为研究对象,设每秒喷出的质量为Δm,火箭对这部分气体的作用力为F,由动量定理有 FΔt=Δmv 0 ①
火箭刚要升空时对地速度为零,此时气体相对火箭的速度也就是气体对地的速度,气体对火箭的反作用力F′=F.对火箭(因忽略气体的重力)F′="Mg " ②
由①②两式解得
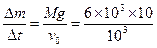 kg/s="60" kg/s
kg/s="60" kg/s
即要获得克服火箭重力的推力,每秒要喷出60 kg的气体.
(2)同第(1)问,以喷出的气体Δm为对象.
FΔt=Δmv 0 ③
而对火箭F-Mg="Ma " ④
由③④两式解得
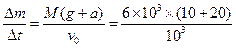 kg/s="180" kg/s.
kg/s="180" kg/s.
【简答题】

[8/63]不定项选择 小车上装有一桶水,静止在光滑水平地面上,如图所示,桶的前、后底及侧面各装有一个阀门,分别为S1、S2、S3、S4(图中未全画出),要使小车...
参考答案:
| B |
参考解析:
无
【简答题】

[9/63]质量为4 t的火箭,其喷出气体对地的速度为500 m/s,则: (1)它至少每秒喷出质量为多少的气体,才能开始上升? (2)如果要以2 m/s 2的加...
参考答案:
|
(1)78.4 kg (2)93.8 kg (3)减小
|
参考解析:
(1)当喷出的气体对火箭的平均冲力大于重力时,火箭才能开始上升.由F=
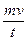 >(M-m)g,t="1" s,得m>
>(M-m)g,t="1" s,得m>
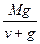 +g="78.4" kg.
+g="78.4" kg.
(2)设a="2" m/s 2时,每秒喷出气体的质量为m′,则由牛顿运动定律得,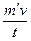 -(M-m′)g=(M-m′)a,t="1" s,求出m′=
-(M-m′)g=(M-m′)a,t="1" s,求出m′=
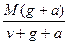 ="93.8" kg.
="93.8" kg.
(3)由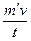 -(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=
-(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=
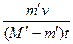 -g=
-g=
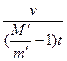 -g,要使a 保持不变,只有使每秒喷出气体的质量m′减小.
-g,要使a 保持不变,只有使每秒喷出气体的质量m′减小.
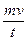 >(M-m)g,t="1" s,得m>
>(M-m)g,t="1" s,得m>
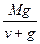 +g="78.4" kg.
+g="78.4" kg.
(2)设a="2" m/s 2时,每秒喷出气体的质量为m′,则由牛顿运动定律得,
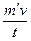 -(M-m′)g=(M-m′)a,t="1" s,求出m′=
-(M-m′)g=(M-m′)a,t="1" s,求出m′=
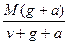 ="93.8" kg.
="93.8" kg.
(3)由
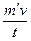 -(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=
-(M′-m′)g=(M′-m′)a分析知,火箭上升过程中,总质量M′在不断减小,(M′-m′)不断减小,a=
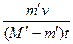 -g=
-g=
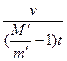 -g,要使a 保持不变,只有使每秒喷出气体的质量m′减小.
-g,要使a 保持不变,只有使每秒喷出气体的质量m′减小.
【简答题】

[10/63]一个静止的质量为M的不稳定原子核,放射出一个质量为m的粒子,粒子离开原子核时相对原子核的速度为v0,则原子核剩余部分的速率等于____。
参考答案:
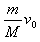 |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





