
创建自己的小题库
搜索

用向量证明线线、线面、面面的垂直、平行关系题库
题数
1139
考试分类
高中数学>用向量证明线线、线面、面面的垂直、平行关系
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-用向量证明线线、线面、面面的垂直、平行关系
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/1139]如图所示,直线 【图片】垂直于⊙ 【图片】所在的平面, 【图片】内接于⊙ 【图片】,且 【图片】为⊙ 【图片】的直径,点 【图片】为线段 【图片】的中...
参考答案:
|
B
|
参考解析:
对于结论①,由于
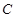 是以
是以
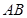 为直径的圆
为直径的圆
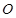 上一点,所以
上一点,所以
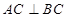 ,因为
,因为
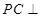 平面
平面
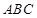 ,于是可以得到
,于是可以得到
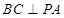 ,结合直线与平面垂直的判定定理可以得到
,结合直线与平面垂直的判定定理可以得到
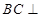 平面
平面
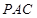 ,因此
,因此
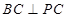 ,所以结论①正确;对于结论②,由于
,所以结论①正确;对于结论②,由于
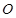 、
、
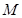 分别为
分别为
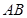 、
、
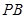 的中点,由中位线原理可知
的中点,由中位线原理可知
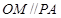 ,利用直线与平面平行的判定定理可以得到
,利用直线与平面平行的判定定理可以得到
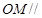 平面
平面
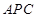 ,所以结论②正确;对于结论③,由结论①知,
,所以结论②正确;对于结论③,由结论①知,
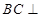 平面
平面
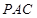 ,所以结论③正确,故选B.
,所以结论③正确,故选B.
【简答题】

[2/1139](满分14分)如图在三棱锥 【图片】中, 【图片】分别为棱 【图片】的中点,已知 【图片】, 【图片】求证(1)直线 【图片】平面 【图片】; (2)...
参考答案:
|
证明见解析.
|
参考解析:
(1)本题证明线面平行,根据其判定定理,需要在平面
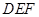 内找到一条与
内找到一条与
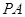 平行的直线,由于题中中点较多,容易看出
平行的直线,由于题中中点较多,容易看出
 ,然后要交待
,然后要交待
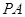 在平面
在平面
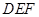 外,
外,
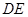 在平面
在平面
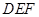 内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得
内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得
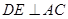 ,因此考虑能否证明
,因此考虑能否证明
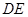 与平面
与平面
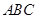 内的另一条与
内的另一条与
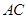 相交的直线垂直,由已知三条线段的长度,可用勾股定理证明
相交的直线垂直,由已知三条线段的长度,可用勾股定理证明
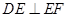 ,因此要找的两条相交直线就是
,因此要找的两条相交直线就是
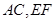 ,由此可得线面垂直.
,由此可得线面垂直.
(1)由于
 分别是
分别是
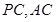 的中点,则有
的中点,则有
 ,又
,又
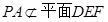 ,
,
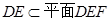 ,所以
,所以
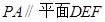 .
.
(2)由(1)
 ,又
,又
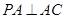 ,所以
,所以
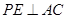 ,又
,又
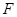 是
是
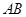 中点,所以
中点,所以
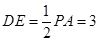 ,
,
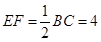 ,
,
 又
又
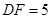 ,所以
,所以
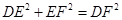 ,所以
,所以
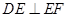 ,
,
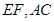 是平面
是平面
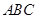 内两条相交直线,所以
内两条相交直线,所以
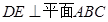 ,又
,又
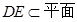
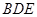 ,所以平面
,所以平面
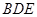
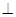 平面
平面
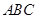 .
.
【考点】线面平行与面面垂直.
【简答题】

[3/1139]如图,正方形 【图片】所在平面与圆 【图片】所在的平面相交于 【图片】,线段 【图片】为圆 【图片】的弦, 【图片】垂直于圆 【图片】所在的平面,垂足...
参考答案:
|
(1)详见解析;(2)详见解析.
|
参考解析:
(1)证明平面
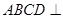 平面
平面
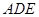 ,即证明
,即证明
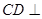 平面
平面
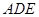 ,转化为证明直线
,转化为证明直线
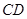 与平面
与平面
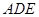 内的两条相交直线垂直;(2)立体几何中求空间角的方法有两种,一是常规法,找出(或作出)适合题意的角;证明找出的角符合对应角的要求;求出相关角的大小(或三角函数值).二是用向量法,即先确定两个向量(直线的方向向量或平面的法向量)求两个向量夹角的余弦值,注意确定所求的夹角与向量夹角的关系,最后得出所求的角或角的三角函数值.
内的两条相交直线垂直;(2)立体几何中求空间角的方法有两种,一是常规法,找出(或作出)适合题意的角;证明找出的角符合对应角的要求;求出相关角的大小(或三角函数值).二是用向量法,即先确定两个向量(直线的方向向量或平面的法向量)求两个向量夹角的余弦值,注意确定所求的夹角与向量夹角的关系,最后得出所求的角或角的三角函数值.
(1)
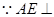 圆
圆
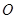 所在的平面,
所在的平面,
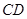 在圆
在圆
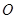 所在的平面上,
所在的平面上,
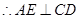 ,
,
又在正方形
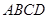 中,
中,
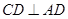 ,
,
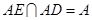 ,
,
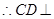 平面
平面
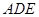 ,
,
又
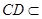 平面
平面
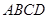 ,
,
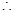 平面
平面
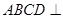 平面
平面
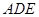 .
.
(2)
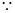
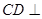 平面
平面
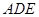 ,
,
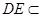 平面
平面
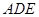 ,
,
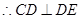 ,即
,即
 为圆
为圆
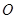 的直径,
的直径,
又
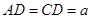 ,且
,且
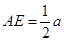 ,
,
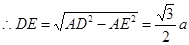 ,
,
以点
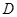 为坐标原点,分别以
为坐标原点,分别以
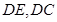 为
为
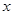 轴、
轴、
 轴,以垂直于底面
轴,以垂直于底面
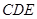 的直线为
的直线为
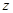 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则
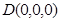 ,
,
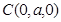 ,
,
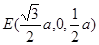 ,
,
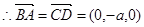 ,
,
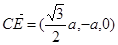 ,
,
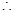
 ,
,
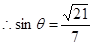 ,
,
又
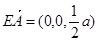 ,
,
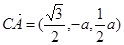 ,
,
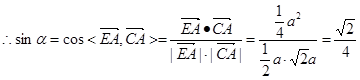 ,
,
由此得
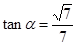 ,
,
设平面
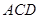 的一个法向量
的一个法向量
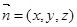 ,则
,则
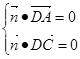 ,即
,即
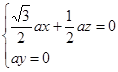 ,
,
取
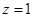 ,则
,则
 ,又平面
,又平面
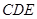 的一个法向量为
的一个法向量为
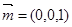 ,
,
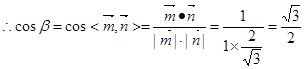 ,
,
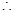
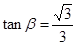 ,
,
于是
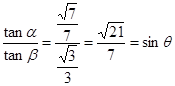 ,即
,即
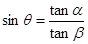 .
.
【简答题】

[4/1139]已知 【图片】为直线, 【图片】为平面,给出下列命题: 【图片】① 【图片】 ② 【图片】 ③ 【图片】 ④ 【图片】 ...
参考答案:
|
B
|
参考解析:
略
【简答题】

[5/1139]如图,三棱锥P ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点 【图片】(1)若PA=2,求直线AE与PB所...
参考答案:
|
(1)
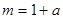 , ,
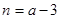 ;(2) ;(2)
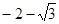
|
参考解析:
(1)首先建立空间直角坐标系,给出相关点的坐标,利用空间向量求解;(2) 利用空间向量求解平面的法向量,然后根据法向量互相垂直可证明
(1)如图,取AC的中点F,连接BF,则BF⊥AC 以A为坐标原点,过A且与FB平行的直线为x轴,AC为y轴,AP为z轴,建立空间直角坐标系

则A(0,0,0),B(,1,0), C(0,2,0),P(0,0,2),E(0,1,1),
从而=(,1, 2), =(0,1,1)
设直线AE与PB所成角为θ,
则cosθ=||=
即直线AE与PB所成角的余弦值为 5分
(2)如上图,则
A(0,0,0),B(,1,0), C(0,2,0),P(0,0,),E(0,1,
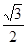 ),
),
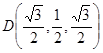
设平面PBC的法向量为
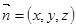 ,则
,则
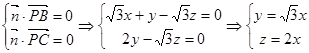
令
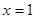 ,则
,则
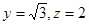 ,所以
,所以
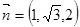
同理可求平面ADE的法向量
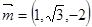
所以
 ,即
,即
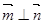
于是平面ADE⊥平面PBC
【简答题】

[6/1139]如图,在正三棱柱 【图片】中, 【图片】, 【图片】分别为 【图片】, 【图片】的中点. 【图片】(1)求证: 【图片】平面 【图片】; (2)求证:...
参考答案:
|
(1)详见解析;(2)详见解析.
|
参考解析:
(1)要证线面平行,需有线线平行.由
 ,
,
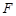 分别为
分别为
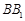 ,
,
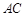 的中点,想到取
的中点,想到取
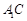 的中点
的中点
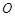 ;证
;证
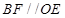 就成为解题方向,这可利用平行四边形来证明.在由线线平行证线面平行时,需完整表示定理条件,尤其是线在面外这一条件;(2)要证面面垂直,需有线面垂直.由正三棱柱性质易得底面
就成为解题方向,这可利用平行四边形来证明.在由线线平行证线面平行时,需完整表示定理条件,尤其是线在面外这一条件;(2)要证面面垂直,需有线面垂直.由正三棱柱性质易得底面
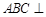 侧面
侧面
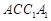 ,
,
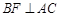 ,从而
,从而
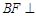 侧面
侧面
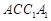 ,而
,而
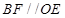 ,因此有线面垂直:
,因此有线面垂直:
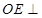 面
面
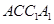 .在面面垂直与线面垂直的转化过程中,要注意充分应用几何体及平面几何中的垂直条件.
.在面面垂直与线面垂直的转化过程中,要注意充分应用几何体及平面几何中的垂直条件.
(1)连
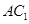 交
交
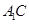 于点
于点
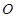 ,
,
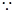
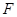 为
为
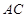 中点,
中点,
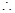
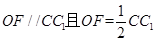 ,
,
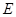 为
为
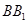 中点,
中点,
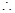
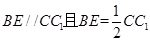 ,
,
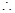
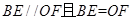 ,
,
 四边形
四边形
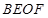 是平行四边形, 4分
是平行四边形, 4分
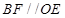 ,又
,又
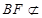 平面
平面
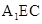 ,
,
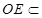 平面
平面
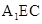 ,
,
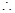
 平面
平面
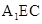 . 7分
. 7分
(2)由(1)知
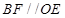 ,
,
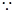
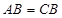 ,
,
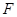 为
为
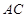 中点,所以
中点,所以
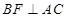 ,所以
,所以
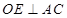 , 9分
, 9分
又因为
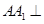 底面
底面
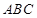 ,而
,而
 底面
底面
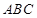 ,所以
,所以
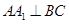 ,
,
则由
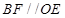 ,得
,得
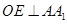 ,而
,而
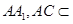 平面
平面
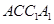 ,且
,且
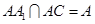 ,
,
所以
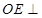 面
面
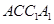 , 12分
, 12分
又
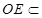 平面
平面
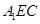 ,所以平面
,所以平面
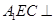 平面
平面
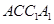 . 14分
. 14分
【简答题】

[7/1139]E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则AC与平面EFGH的位置关系是 &nbs...
参考答案:
|
平行
|
参考解析:
解:利用三角形的中位线平行于底边,我们可以得到线线平行,再利用线面平行的判定定理得到结论。
【简答题】

[8/1139]如图, 【图片】是 【图片】的直径, 【图片】垂直于 【图片】所在的平面, 【图片】是圆周上不同于 【图片】的任意一点,则图中直角三角形有 ...
参考答案:
|
4个
|
参考解析:
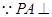 平面
平面
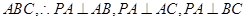 ,则
,则
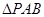 和
和
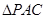 是直角三角形;
是直角三角形;
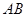 是
是
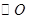 的直径,
的直径,
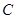 是圆周上不同于
是圆周上不同于
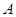 、
、
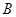 的任意一点,所以
的任意一点,所以
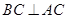 ,
,
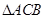 是直角三角形;又
是直角三角形;又
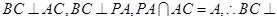 平面
平面
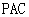 ,
,
 ,则
,则
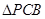 是直角三角形;故直角三角形有4个.
是直角三角形;故直角三角形有4个.
【简答题】

[9/1139]如图. 直三棱柱ABC —A 1B 1C 1中,A 1B 1= A 1C 1,点D、E分别是棱BC,CC 1上的点(点D不同于点C),且AD⊥DE,F...
参考答案:
|
(1)详见解析;(2)详见解析.
|
参考解析:
(1)由面面垂直的判定定理可知:要证两个平面互相垂直,只须证明其中一个平面内的一条直线与另一个平面垂直即可;观察图形及已知条件可知:只须证平面ADE内的直线AD与平面BCC 1B 1垂直即可;而由已知有: AD⊥DE,又在直三棱柱中易知CC 1⊥面ABC,而AD
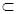 平面ABC,
平面ABC,
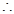 CC
1⊥AD,从而有AD⊥面B CC
1 B
1,所以有平面ADE⊥平面BCC
1B
1;(2)由线面平行的判定定理可知:要证线面平行,只须证明直线与平面内的某一条直线平行即可;不难发现只须证明A
1F∥AD,由(1)知AD⊥面B CC
1 B
1,故只须证明A
1F⊥平面BCC
1B
1,这一点很容易获得.
CC
1⊥AD,从而有AD⊥面B CC
1 B
1,所以有平面ADE⊥平面BCC
1B
1;(2)由线面平行的判定定理可知:要证线面平行,只须证明直线与平面内的某一条直线平行即可;不难发现只须证明A
1F∥AD,由(1)知AD⊥面B CC
1 B
1,故只须证明A
1F⊥平面BCC
1B
1,这一点很容易获得.
(1)
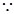 ABC—A
1B
1C
1是直三棱柱,
ABC—A
1B
1C
1是直三棱柱,
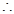 CC
1⊥面ABC,
CC
1⊥面ABC,
又AD
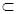 平面ABC,
平面ABC,
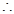 CC
1⊥AD
CC
1⊥AD
又
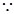 AD⊥DE,CC
1,DE
AD⊥DE,CC
1,DE
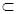 平面B CC
1B
1,CC
1∩DE=E
平面B CC
1B
1,CC
1∩DE=E
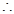 AD⊥面B CC
1 B
1又AD
AD⊥面B CC
1 B
1又AD
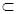 面ADE
面ADE
 平面ADE⊥平面BCC
1B
1 6分
平面ADE⊥平面BCC
1B
1 6分
(2)
 A
1B
1= A
1C
1,F为B
1C
1的中点,
A
1B
1= A
1C
1,F为B
1C
1的中点,
 AF⊥B
1C
1
AF⊥B
1C
1
 CC
1⊥面A
1B
1C
1且A,F
CC
1⊥面A
1B
1C
1且A,F
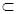 平面A
1B
1C
1
平面A
1B
1C
1
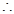 CC
1⊥A、F
CC
1⊥A、F
又CC 1,A,F
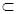 平面BCC
1B
1,CC
1∩B
1C
1= C
1
平面BCC
1B
1,CC
1∩B
1C
1= C
1
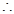 A
1F⊥平面BCC
1B
1 由(1)知AD ⊥平面BCC
1B
1
A
1F⊥平面BCC
1B
1 由(1)知AD ⊥平面BCC
1B
1
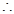 A
1F∥AD,又AD
A
1F∥AD,又AD
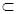 平面ADE,A
1F
平面ADE,A
1F
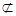 平面ADE
平面ADE
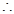 A
1F∥平面ADE 12分
A
1F∥平面ADE 12分
【简答题】

[10/1139]在四棱锥 P- ABCD中,底面 ABCD是边长为1的正方形,且 PA⊥平面 ABCD. 【图片】 (1)求证: PC⊥ BD; (2)过...
参考答案:
|
(1)见解析(2)
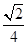 , ,
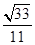
|
参考解析:
(1)连接
AC,因为四边形
ABCD是正方形,所以
BD⊥
AC.因为
PA⊥平面
ABCD,所以
PA⊥
BD.
又 AC∩ PA= A,所以 BD⊥平面 PAC.
又 PC⊂平面 PAC,所以 PC⊥ BD.
(2)解 ①设 PA= x,三棱锥 E- BCD的底面积为定值,在△ PBC中,易知 PB=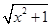 ,
PC=
,
PC=
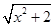 ,
,
又 BC=1,故△ PBC直角三角形.又 BE⊥ PC,得 EC=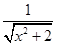 ,可求得该三棱锥的高
h=
,可求得该三棱锥的高
h=
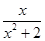 =
=
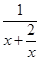 .
.
当且仅当 x=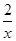 ,即
x=
,即
x=
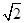 时,三棱锥
E-
BCD的体积取到最大值,所以
h=
时,三棱锥
E-
BCD的体积取到最大值,所以
h=
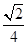 .
.
此时四棱锥 E- ABCD的高为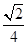 .
.
②以点 A为原点, AB, AD, AP所在直线为坐标轴建立空间直角坐标系,则 A(0,0,0), C(1,1,0), D(0,1,0), P(0,0,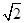 ),易求得
CE=
),易求得
CE=
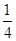 CP.
CP.
所以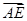 =
=
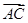 +
+
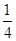
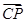 =
=
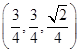 ,
,
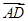 =(0,1,0).
=(0,1,0).
设平面 ADE的法向量 n 1=( x, y, z),则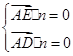
即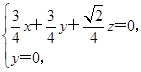 ,令
x=
,令
x=
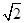 ,则
n
1=(
,则
n
1=(
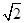 ,0,-3),
,0,-3),
同理可得平面 BDE的法向量 n 2=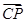 =(-1,-1,
=(-1,-1,
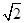 ),所以cos〈
n
1,
n
2〉=
),所以cos〈
n
1,
n
2〉=
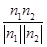 =-
=-
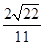 .所以sin〈
n
1,
n
2〉=
.所以sin〈
n
1,
n
2〉=
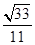 .所以二面角
A-
DE-
B的正弦值的大小为
.所以二面角
A-
DE-
B的正弦值的大小为
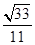 .
.
又 AC∩ PA= A,所以 BD⊥平面 PAC.
又 PC⊂平面 PAC,所以 PC⊥ BD.
(2)解 ①设 PA= x,三棱锥 E- BCD的底面积为定值,在△ PBC中,易知 PB=
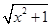 ,
PC=
,
PC=
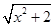 ,
,
又 BC=1,故△ PBC直角三角形.又 BE⊥ PC,得 EC=
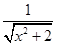 ,可求得该三棱锥的高
h=
,可求得该三棱锥的高
h=
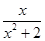 =
=
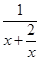 .
.
当且仅当 x=
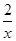 ,即
x=
,即
x=
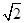 时,三棱锥
E-
BCD的体积取到最大值,所以
h=
时,三棱锥
E-
BCD的体积取到最大值,所以
h=
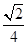 .
.
此时四棱锥 E- ABCD的高为
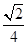 .
.
②以点 A为原点, AB, AD, AP所在直线为坐标轴建立空间直角坐标系,则 A(0,0,0), C(1,1,0), D(0,1,0), P(0,0,
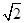 ),易求得
CE=
),易求得
CE=
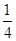 CP.
CP.
所以
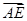 =
=
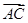 +
+
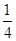
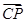 =
=
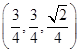 ,
,
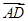 =(0,1,0).
=(0,1,0).
设平面 ADE的法向量 n 1=( x, y, z),则
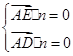
即
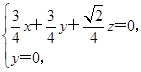 ,令
x=
,令
x=
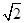 ,则
n
1=(
,则
n
1=(
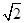 ,0,-3),
,0,-3),
同理可得平面 BDE的法向量 n 2=
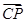 =(-1,-1,
=(-1,-1,
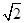 ),所以cos〈
n
1,
n
2〉=
),所以cos〈
n
1,
n
2〉=
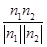 =-
=-
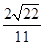 .所以sin〈
n
1,
n
2〉=
.所以sin〈
n
1,
n
2〉=
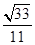 .所以二面角
A-
DE-
B的正弦值的大小为
.所以二面角
A-
DE-
B的正弦值的大小为
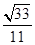 .
.

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





