
创建自己的小题库
搜索

全称量词与存在性量词题库
题数
609
考试分类
高中数学>全称量词与存在性量词
售价
¥25
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-全称量词与存在性量词
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/609]已知命题p:“ 【图片】x∈R,x2-x+1>0,则命题 【图片】p是( )。
参考答案:
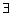 x∈R,x2-x+1≤0 x∈R,x2-x+1≤0 |
参考解析:
无
【简答题】

[2/609]命题“存在正实数x,使得lgx≤1”的否定是( )
参考答案:
| 任意正实数x>0,使得lgx>1 |
参考解析:
无
【简答题】

[3/609]命题“∀x∈R,tan(-x)=tanx.”的否定是______.
参考答案:
| 命题“∀x∈R,tan(-x)=tanx.”是个全称命题, 否定是∃x∈R,tan(-x)≠tanx. 故答案为:∃x∈R,tan(-x)≠tanx. |
参考解析:
无
【简答题】

[4/609]已知命题P:∀x>2,x3-8>0,那么¬P是( ) A.∀x≤2,x3-8≤0B.∃x>2,x3-8≤0C.∀x>2,x3-8≤0D.∃x≤2,x...
参考答案:
| 命题P为全称命题,其否定为特称命题, 则¬P:∃x≤2,x3-8≤0, 故选D. |
参考解析:
无
【简答题】

[5/609]不等式x2-x>x-a对∀x∈R都成立,则a的取值范围是______.
参考答案:
| 法一:不等式x2-x>x-a对∀x∈R都成立,即不等式x2-2x+a>0恒成立; 结合二次函数图象得对应方程的△<0,即4-4a<0,所以a>1. 法二:不等式x2-x>x-a对∀x∈R都成立, 也可看作a>-x2+2x对∀x∈R都成立, 所以a>(-x2+2x)max;而二次函数f(x)=-x2+2x的最大值为
所以a>1. 故答案为:a>1. |
参考解析:
无
【简答题】

[6/609]命题“∀x∈R,x2-x+1>0”的否定是______.
参考答案:
| ∵命题“∀x∈R,x2-x+1>0” ∵“任意”的否定为“存在” ∴命题的否定为:∃x0∈R,x02-x0+1≤0, 故答案为:∃x0∈R,x02-x0+1≤0 |
参考解析:
无
【简答题】

[7/609]已知命题 p: 【图片】x∈R,x≥2,那么命题 【图片】p为 [ ...
参考答案:
| D |
参考解析:
无
【简答题】

[8/609]对于下述命题p,写出“¬p”形式的命题,并判断“p”与“¬p”的真假:(1)p:91∈(A∩B)(其中全集U=N*,A=x|x是质数,B=x|x是正奇...
参考答案:
| (1)?p:91?A,或91?B;p真,?p假; (2)?p:每一个素数都不是偶数;p真,?p假; (3)?p:存在一个正整数不是质数且不是合数;p假,?p真; (4)?p:存在一个三角形有两个以上的外接圆或没有外接圆. |
参考解析:
无
【简答题】

[9/609]对于命题p:存在x0∈R,使得3x0+x0<0的否定命题是______.
参考答案:
| 命题“存在x0∈R,使得3x0+x0<0”是一个特称命题, 其否定是一个全称命题, 即命题“存在x0∈R,使得3x0+x0<0”的否定是:∀x∈R,3x+x≥0. 故答案为:∀x∈R,3x+x≥0. |
参考解析:
无
【简答题】

[10/609]命题“∃x∈R,x2-2x=0”的否定是( ) A.∀x∈R,x2-2x=0 B.∃x∈R,x2-2x≠0 C.∀x∈R,x2-2x≠0 D.∃x∈...
参考答案:
| C |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





