
创建自己的小题库
搜索

柱体、椎体、台体的表面积与体积题库
题数
2000
考试分类
高中数学>柱体、椎体、台体的表面积与体积
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-柱体、椎体、台体的表面积与体积
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]己知某几何体的三视图如图所示,则其体积为 【图片】 [ ] A.4 B.8&nb...
参考答案:
| A |
参考解析:
无
【简答题】

[2/2000](本小题满分12分)如图,已知四棱锥 【图片】中,底面 【图片】是直角梯形, 【图片】, 【图片】 【图片】, 【图片】, 【图片】, 【图片】平面 ...
参考答案:
|
(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)
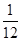
|
参考解析:
本试题主要是考查了立体几何中线面平行和线面垂直的判定定理的运用,以及棱锥的体积公式计算的综合问题。
(1)因为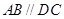 ,结合线面平行的判定定理得到结论。
,结合线面平行的判定定理得到结论。
(2)根据在直角梯形 中,过
中,过
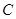 作
作
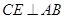 于点
于点
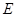 ,
,
则四边形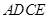 为矩形,∴
为矩形,∴
 ,进而分析得到
,进而分析得到
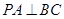 是解决该试题的关键,
是解决该试题的关键,
(3)∵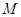 是
是
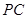 中点,∴
中点,∴
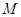 到面
到面
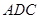 的距离是
的距离是
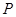 到面
到面
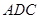 距离的一半,那么利用底面积和高得到体积。
距离的一半,那么利用底面积和高得到体积。
证明:(Ⅰ)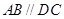 …………… 1分
…………… 1分
又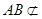 平面
平面
 …………… 2分
…………… 2分
 平面
平面
 …………… 3分
…………… 3分
∴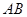 ∥平面
∥平面
 …………… 4分
…………… 4分
(Ⅱ)在直角梯形 中,过
中,过
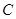 作
作
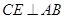 于点
于点
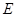 ,
,
则四边形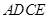 为矩形,∴
为矩形,∴
 ………… 5分
………… 5分
又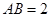 ,∴
,∴
 ,在
,在
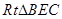 中,
中,
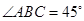 ∴
∴
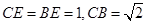 ,∴
,∴
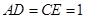
则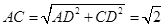 ,
,
 ∴
∴
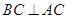 ………… 7分
………… 7分
又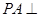 平面
平面
 , ∴
, ∴
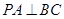 ………… 8分
………… 8分
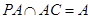 ∴
∴
 平面
平面
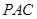 …………… 9分
…………… 9分
(Ⅲ)∵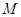 是
是
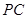 中点,∴
中点,∴
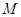 到面
到面
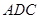 的距离是
的距离是
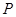 到面
到面
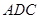 距离的一半……… 10分
距离的一半……… 10分
 …………… 12分
…………… 12分
(1)因为
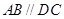 ,结合线面平行的判定定理得到结论。
,结合线面平行的判定定理得到结论。
(2)根据在直角梯形
 中,过
中,过
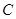 作
作
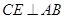 于点
于点
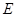 ,
,
则四边形
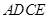 为矩形,∴
为矩形,∴
 ,进而分析得到
,进而分析得到
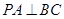 是解决该试题的关键,
是解决该试题的关键,
(3)∵
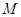 是
是
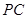 中点,∴
中点,∴
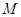 到面
到面
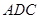 的距离是
的距离是
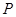 到面
到面
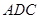 距离的一半,那么利用底面积和高得到体积。
距离的一半,那么利用底面积和高得到体积。
证明:(Ⅰ)
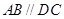 …………… 1分
…………… 1分
又
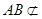 平面
平面
 …………… 2分
…………… 2分
 平面
平面
 …………… 3分
…………… 3分
∴
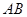 ∥平面
∥平面
 …………… 4分
…………… 4分
(Ⅱ)在直角梯形
 中,过
中,过
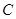 作
作
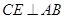 于点
于点
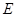 ,
,
则四边形
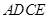 为矩形,∴
为矩形,∴
 ………… 5分
………… 5分
又
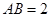 ,∴
,∴
 ,在
,在
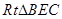 中,
中,
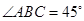 ∴
∴
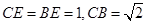 ,∴
,∴
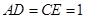
则
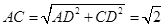 ,
,
 ∴
∴
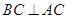 ………… 7分
………… 7分
又
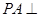 平面
平面
 , ∴
, ∴
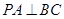 ………… 8分
………… 8分
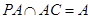 ∴
∴
 平面
平面
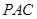 …………… 9分
…………… 9分
(Ⅲ)∵
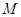 是
是
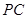 中点,∴
中点,∴
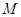 到面
到面
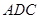 的距离是
的距离是
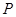 到面
到面
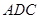 距离的一半……… 10分
距离的一半……… 10分
 …………… 12分
…………… 12分
【简答题】

[3/2000].(本小题满分6分) 如图是一个几何体的三视图(单位:cm) 【图片】(Ⅰ)画出这个几何体的直观图(不要求写画法); (Ⅱ)求这个几何体的表面积及体积...
参考答案:
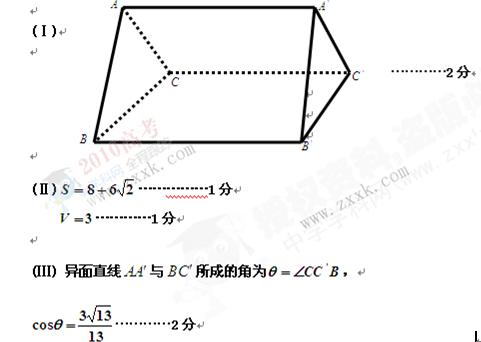
|
参考解析:
略
【简答题】

[4/2000](12分) 如图8-12,球面上有四个点P、A、B、C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积。 【图...
参考答案:
|
解 如图8-12,设过A、B、C三点的球的截面圆半径为r,圆心为O′,球心到该圆面的距离为d。在三棱锥P—ABC中,
∵PA,PB,PC两两互相垂直,且PA=PB=PC=a, ∴AB=BC=CA= 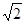 a,且P在△ABC内的射影即是△ABC的中心O′。 a,且P在△ABC内的射影即是△ABC的中心O′。
由正弦定理,得  =2r,∴r= =2r,∴r=
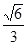 a。 a。
又根据球的截面的性质,有OO′⊥平面ABC,而PO′⊥平面ABC, ∴P、O、O′共线,球的半径R= 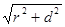 。又PO′= 。又PO′=
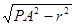 = =
 = =
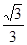 a, a,
∴OO′="R" - 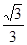 a=d= a=d=
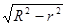 ,(R- ,(R-
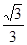 a)
2=R
2 – ( a)
2=R
2 – (
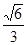 a)
2,解得R= a)
2,解得R=
 a, a,
∴S 球=4πR 2=3πa 2。 |
参考解析:
略
【简答题】

[5/2000]设直线 【图片】与球O有且仅有一公共点P,从直线 【图片】出发的两个半平面截球O的两个截面圆O 1和圆O 2的半径1和2,若这两个半平面 【图片】, ...
参考答案:
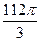
|
参考解析:
略
【简答题】

[6/2000]如图,将一个长方体沿相邻三个面的对角线截出一个棱锥,求棱锥的体积与剩下的几何体体积的比. 【图片】
参考答案:

|
参考解析:
长方体的三条棱长分别为
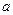 ,
,
 ,
,
 ,
,
则截出的棱锥的体积为 .
.
剩下的几何体的体积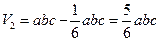 ,所以,
,所以,
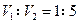 .
.
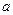 ,
,
 ,
,
 ,
,
则截出的棱锥的体积为
 .
.
剩下的几何体的体积
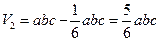 ,所以,
,所以,
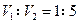 .
.
【简答题】

[7/2000]湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下了一个半径为6 cm,深2 cm的空穴,则该球表面积为( &nbs...
参考答案:
|
A
|
参考解析:
如图,
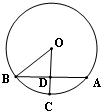
设球心为
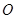 ,
,
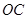 是与冰面垂直的一条球半径,冰面截球得到的小圆圆心为
是与冰面垂直的一条球半径,冰面截球得到的小圆圆心为
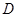 ,
,
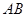 为小圆
为小圆
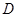 的一条直径,设球的半径为
的一条直径,设球的半径为
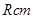 ,则
,则
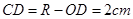 ,∴
,∴
 中,
中,
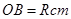 ,
,
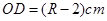 ,
,
 .根据勾股定理,得
.根据勾股定理,得
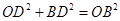 ,即
,即
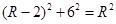 ,解之得
,解之得
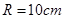 ,∴该球表面积为
,∴该球表面积为
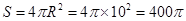 ,故选A.
,故选A.
【简答题】

[8/2000]如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。 【图片】
参考答案:
解:因为 (cm3), (cm3), (cm3), (cm3),因为  , ,所以,冰淇淋融化了,不会溢出杯子。 |
参考解析:
无
【简答题】

[9/2000]如图,已知一四棱锥P-ABCD的底面是边长为1的正方形,且侧棱PC⊥底面ABCD,且PC=2,E是侧棱PC上的动点 (1)求四棱锥P-ABCD的体积;...
参考答案:
|
(1)
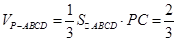 ;(2)见解析;(3) ;(2)见解析;(3)
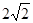 . .
|
参考解析:
(1)根据四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,知高为PC="2." 应用体积计算公式即得;
(2)连结AC,根据ABCD是正方形,得到BD⊥AC ,由PC⊥底面ABCD 得到BD⊥PC,推出BD⊥平面PAC;由于不论点E在何位置,都有AE
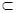 平面PAC,故得BD⊥AE;
平面PAC,故得BD⊥AE;
(3)设
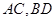 相交于
相交于
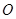 ,连
,连
 ,可知
,可知
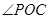 是二面角P-BD-C的的一个平面角,计算其正切即得二面角P-BD-C的正切值.
是二面角P-BD-C的的一个平面角,计算其正切即得二面角P-BD-C的正切值.
(1)该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC="2."
∴
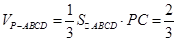 4分
4分
(2)连结AC,∵ABCD是正方形
∴BD⊥AC ∵PC⊥底面ABCD 且
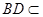 平面
平面
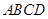 ∴BD⊥PC
∴BD⊥PC
又∵
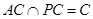 ∴BD⊥平面PAC
∴BD⊥平面PAC
∵不论点E在何位置,都有AE
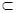 平面PAC
平面PAC
∴BD⊥AE 8分
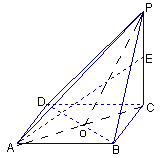
(3)设
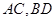 相交于
相交于
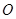 ,连
,连
 ,由四棱锥P-ABCD的底面是边长为1的正方形,PC⊥底面ABCD知,
,由四棱锥P-ABCD的底面是边长为1的正方形,PC⊥底面ABCD知,
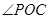 是二面角P-BD-C的的一个平面角,
是二面角P-BD-C的的一个平面角,
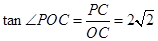 ,即二面角P-BD-C的正切值为
,即二面角P-BD-C的正切值为
 .
.
【简答题】

[10/2000]设三棱锥的3个侧面两两互相垂直,且侧棱长均为2 3,则其外接球的表面积为______.
参考答案:
三棱锥的三条侧棱两两互相垂直,且侧棱长均为2
所以它的外接球就是它扩展为正方体的外接球, 所以求出正方体的对角线的长为:2
所以球的直径是6,半径为3, 所以球的表面积为:4π×32=36π. 故答案为36π. |
参考解析:
3

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





