创建自己的小题库
搜索

简单随机抽样题库
题数
714
考试分类
高中数学>简单随机抽样
售价
¥25
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-简单随机抽样
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/714]为了调查某班级的作业完成的情况,将该班级的52名学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知5号、31号、44号同学在样本中,那么样本中...
参考答案:
|
C
|
参考解析:
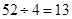 ,所以每相邻两个数之间隔为13,所以选C.
,所以每相邻两个数之间隔为13,所以选C.
【简答题】

[2/714]一个年级有12个班,每个班从1-50排学号,为了交流学习经验,要求每班的14参加交流活动,这里运用的抽样方法是( ) A.简单随抽样B.抽签法C.随...
参考答案:
| 当总体容量N较大时,采用系统抽样.将总体分段,分段的间隔要求相等,这时间隔一般为预先制定的,在第1段内采用简单随机抽样确定一个起始编号,在此编号的基础上加上分段间隔的整倍数即为抽样编号.将总体均分后的每一部分进行抽样时,采用的是简单随机抽样;这是一个几种方法结合的题目. 故选D |
参考解析:
无
【简答题】

[3/714]为了了解参加运动会的2000名运动员的年龄情况,从中抽取100名运动员.就这个问题,下列说法中正确的有( )。①2...
参考答案:
| ④⑥ |
参考解析:
无
【简答题】

[4/714]欲对某商场作一简要审计,通过检查发票及销售记录的2%来快速估计每月的销售总额.现采用如下方法:从某本50张的发票存根中随机抽一张,如15号,然后按序往...
参考答案:
| ∵总体的个体比较多, 抽样时某本50张的发票存根中随机抽一张,如15号, 这是系统抽样中的分组, 然后按序往后将65号,115号,165号,…发票上的销售额组成一个调查样本. 故选B. |
参考解析:
无
【简答题】

[5/714]. 某校有学生 【图片】人,其中高一学生 【图片】人.为调查学生了解消防知识的现状,采用按年级分层抽样的方法,从该校学生中抽取一个 【图片】人的样本,...
参考答案:
|
16
|
参考解析:
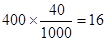
【简答题】

[6/714]某私立学校共有员工160人,其中有任课教师120人,管理人员16人,后勤服务人员24人,为了了解员工的某种情况,要从中抽取一个容量为20的样本.用分层...
参考答案:
|
因为样本容量与总体的容量的比为20∶160=1∶8,
所以在各类人员中抽取的个体数依次是 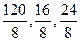 ,即15,2,3. ,即15,2,3.
下面我们利用系统抽样在120名教师中抽取容量为15的样本,假定这120名教师的编号是1,2,…,120,由于15∶120=1∶8,我们将120名教师分成15个部分,每个部分包括8名教师,然后在这15个部分中每一部分抽一个号码,如果它是3号,那么从3号起,每隔8个抽取1个号码,这样得抽得的15位教师的号码为3,11,19,27,35,43,51,59,67,75,83,91,99,107,115. 假定16位管理人员的编号是121,122,…,136,24位后勤服务人员的编号是137,138,…,160.则同理可采用系统抽样法抽出的个体为123,131和139,147,155. 将以上各类人中抽取的个体合在一起,得所要抽取的样本为: 3,11,19,27,35,43,51,59,67,75,83,91,99,107,115,123,131,139,147,155. |
参考解析:
本题考查分层抽样的步骤和方法.
【简答题】

[7/714]一个容量为 【图片】的样本数据,分组后组距与频数如下表: 组距 【图片】 【图片】 【图片】 【图片】 【图片】 【图片】频数234542则样本在区间...
参考答案:
|
0.7
|
参考解析:
解:样本在区间
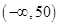 上的频数为2+3+4+5=14,14/20=0.7,即为频率。
上的频数为2+3+4+5=14,14/20=0.7,即为频率。
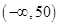 上的频数为2+3+4+5=14,14/20=0.7,即为频率。
上的频数为2+3+4+5=14,14/20=0.7,即为频率。
【简答题】

[8/714]某重点中学高中各班级学生人数如下表所示: 年级班高一年级高二年级高三年级1班4546482班4854553班525052学校计划召开学生代表座谈会.请...
参考答案:
|
由表中基本数据可知,高一学生总数为145人,高二学生总数为150人,高三学生总数为155人,
第一步:确定高一、高二、高三的被抽个体数.由于总体容量与样本容量之比为20,所以样本中包含的各年级个体数应为145÷20≈7,150÷20≈8,155÷20≈8. 第二步:将高一年级被抽到的个体数分配到各班.由于抽样比为 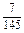 ,所以1班、2班、3班被抽到的人数分别为 ,所以1班、2班、3班被抽到的人数分别为
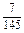 ×45≈2, ×45≈2,
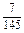 ×48≈2, ×48≈2,
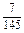 ×52≈3. ×52≈3.
第三步:将高二年级被抽到的个体数分配到各班.由于抽样比为 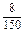 ,所以1班、2班、3班被抽到的人数分别为 ,所以1班、2班、3班被抽到的人数分别为
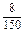 ×46≈2, ×46≈2,
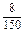 ×54≈3, ×54≈3,
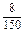 ×50≈3. ×50≈3.
第四步:将高三年级被抽到的个体数分配到各班.由于抽样比为 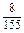 ,所以1班、2班、3班被抽到的人数分别为 ,所以1班、2班、3班被抽到的人数分别为
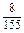 ×48≈2, ×48≈2,
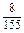 ×55≈3, ×55≈3,
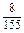 ×52≈3. ×52≈3.
|
参考解析:
由表中基本数据可知,高一学生总数为145人,高二学生总数为150人,高三学生总数为155人,
第一步:确定高一、高二、高三的被抽个体数.由于总体容量与样本容量之比为20,所以样本中包含的各年级个体数应为145÷20≈7,150÷20≈8,155÷20≈8.
第二步:将高一年级被抽到的个体数分配到各班.由于抽样比为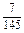 ,所以1班、2班、3班被抽到的人数分别为
,所以1班、2班、3班被抽到的人数分别为
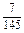 ×45≈2,
×45≈2,
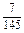 ×48≈2,
×48≈2,
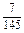 ×52≈3.
×52≈3.
第三步:将高二年级被抽到的个体数分配到各班.由于抽样比为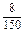 ,所以1班、2班、3班被抽到的人数分别为
,所以1班、2班、3班被抽到的人数分别为
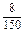 ×46≈2,
×46≈2,
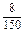 ×54≈3,
×54≈3,
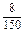 ×50≈3.
×50≈3.
第四步:将高三年级被抽到的个体数分配到各班.由于抽样比为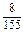 ,所以1班、2班、3班被抽到的人数分别为
,所以1班、2班、3班被抽到的人数分别为
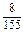 ×48≈2,
×48≈2,
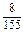 ×55≈3,
×55≈3,
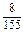 ×52≈3.
×52≈3.
第一步:确定高一、高二、高三的被抽个体数.由于总体容量与样本容量之比为20,所以样本中包含的各年级个体数应为145÷20≈7,150÷20≈8,155÷20≈8.
第二步:将高一年级被抽到的个体数分配到各班.由于抽样比为
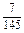 ,所以1班、2班、3班被抽到的人数分别为
,所以1班、2班、3班被抽到的人数分别为
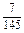 ×45≈2,
×45≈2,
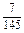 ×48≈2,
×48≈2,
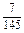 ×52≈3.
×52≈3.
第三步:将高二年级被抽到的个体数分配到各班.由于抽样比为
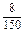 ,所以1班、2班、3班被抽到的人数分别为
,所以1班、2班、3班被抽到的人数分别为
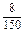 ×46≈2,
×46≈2,
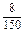 ×54≈3,
×54≈3,
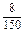 ×50≈3.
×50≈3.
第四步:将高三年级被抽到的个体数分配到各班.由于抽样比为
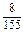 ,所以1班、2班、3班被抽到的人数分别为
,所以1班、2班、3班被抽到的人数分别为
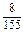 ×48≈2,
×48≈2,
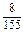 ×55≈3,
×55≈3,
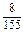 ×52≈3.
×52≈3.
【简答题】

[9/714]据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在...
参考答案:
|
(I)应在“无所谓”态度抽取720×
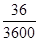 =72人; =72人;
(Ⅱ)ξ的分布列为:
|
参考解析:
ξ
1
2
3
P



1
2
3
P



【简答题】

[10/714]管理人员从一池塘内捞出30条鱼,做上标记后放回池塘.10天后,又从池塘内捞出50条鱼,其中有标记的有2条.根据以上数据可以估计该池塘内共有______...
参考答案:
| 由题意可得:从池塘内捞出50条鱼,其中有标记的有2条, 所有池塘中有标记的鱼的概率为:
又因为池塘内具有标记的鱼一共有30条鱼, 所有可以估计该池塘内共有
故答案为750. |
参考解析:
250

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫