
创建自己的小题库
搜索

一般数列的项题库
题数
251
考试分类
高中数学>一般数列的项
售价
¥20
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-一般数列的项
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/251]数列{an}中, 【图片】,则该数列前100项中的最大项与最小项分别是( ) A.a1,a50 B.a1,a44 C.a4...
参考答案:
| C |
参考解析:
无
【简答题】

[2/251]古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如下图1,2,他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;...
参考答案:
| C |
参考解析:
无
【简答题】

[3/251]已知数列{an}满足a1=1,且对任意n∈N*都有 【图片】,(1)求a2,a3的值;(2)求数列{an}的通项公式;(3)证明: 【图片】(n∈N*...
参考答案:
解:(1)由已知 ,得 ,得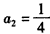 , ,又 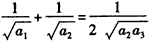 ,得 ,得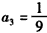 ; ;(2)当n≥2时,  ,① ,①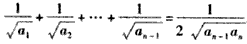 ,② ,②由①-②得 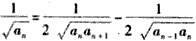 , ,所以 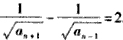 , ,所以数列 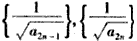 皆为等差数列, 皆为等差数列,所以 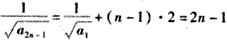 , ,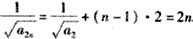 ; ;综上, 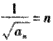 ,所以 ,所以 。 。(3)由(2)得 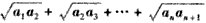 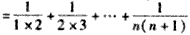 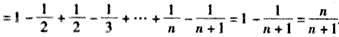 , ,又 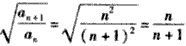 , ,所以等式成立. |
参考解析:
无
【简答题】

[4/251]已知数列 【图片】,……,则 【图片】是数列的( ) A.第18项 B.第19项 C.第17项 D.第20项
参考答案:
| B |
参考解析:
无
【简答题】

[5/251]已知数列{an}的通项公式 【图片】,(1)求a10;(2) 【图片】是否是这个数列中的项? (3)这个数列中有多少整数项?(4)是否有等于序号的项?...
参考答案:
解:(1) ; ;(2)令  ,得n=100, ,得n=100,故是这个数列的第100项。 (3)  , ,∴当n=1,2,3,6时,an为整数故这个数列中有4项是整数项. (4)令  ,得 ,得 , ,解得n=3或n=-2(舍), 故该数列中有等于序号的项,即a3=3。 |
参考解析:
无
【简答题】

[6/251]在数列{an}与{bn}中,a1=1,b1=4,数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0,2an+1为bn与bn+1的等比中项,n...
参考答案:
解:(1)由题设有 ,a1=1,解得 ,a1=1,解得 , ,由题设又有  ,b1=4,解得 ,b1=4,解得 ; ;(2)由题设  ,2an+1为bn与bn+1的等比中项,a1=1,b1=4,及 ,2an+1为bn与bn+1的等比中项,a1=1,b1=4,及 , , , ,进一步可得  , ,猜想  , , ,n∈N*, ,n∈N*,先证  ,n∈N*, ,n∈N*,当n=1时,  ,等式成立; ,等式成立;当n≥2时用数学归纳法证明如下: (1)当n=2时,  ,等式成立; ,等式成立;(2)假设n=k时等式成立,即  ,k≥2, ,k≥2,由题设,  , ① , ①  ,② ,② ①的两边分别减去②的两边,整理得  , ,从而  . .这就是说,当n=k+1时等式也成立. 根据(1)和(2)可知,等式  对任何的n≥2成立. 对任何的n≥2成立.综上所述,等式  对任何的n∈N*都成立; 对任何的n∈N*都成立;再用数学归纳法证明  ,n∈N*。 ,n∈N*。(1)当n=1时,  =4,等式成立; =4,等式成立;(2)假设当n=k时等式成立, 即  ,那么 ,那么 , ,这就是说,当n=k+1时等式也成立. 根据(1)和(2)可知,等式  对任何的n∈N*都成立。 对任何的n∈N*都成立。 |
参考解析:
无
【简答题】

[7/251]已知数列{an}对于任意p,q∈N*有ap+aq=ap+q,若a1= 【图片】,则a36=( )。
参考答案:
| 4 |
参考解析:
无
【简答题】

[8/251]已知数列{an}的前n项和为Sn,且Sn=2an-2,则a2等于 A、4 B、2 C、1 D、-2
参考答案:
| A |
参考解析:
无
【简答题】

[9/251]数列{an}中, 【图片】,且a1=2,则an等于( ) [ &nbs...
参考答案:
| B |
参考解析:
无
【简答题】

[10/251]数列{an}满足an+1= 【图片】,若a1= 【图片】,则a2011= [ ] A. 【图片】B. ...
参考答案:
| B |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





