创建自己的小题库
搜索
排序不等式题库
题数
6
考试分类
高中数学>排序不等式
售价
¥0
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-排序不等式
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/6]若a＜b＜c，x＜y＜z，则下列各式中值最大的一个是（ ） A．ax+cy+bz B．bx+ay+cz C．bx+cy+az D．ax+by+cz
参考答案：
| D |
参考解析：
无
【简答题】
[2/6]（不等式选讲） 已知 a>0, b>0, c>0, abc=1,试证明： 【图片】.
参考答案：
|
略
|
参考解析：
: 证明：由
，
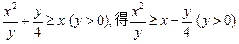所以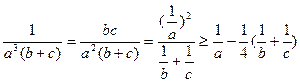
同理：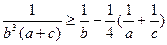
，
相加得：左³
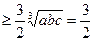……………(10分)
，
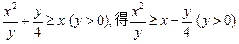所以
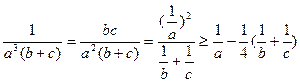
同理：
，
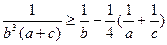相加得：左³
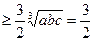……………(10分)
【简答题】
[3/6]设a，b，c是正实数，求证：aabbcc≥（abc）a+b+c3．
参考答案：
| 证明：不妨设a≥b≥c＞0，则lga≥lgb≥lgc． 据排序不等式有： alga+blgb+clgc≥blga+clgb+algc alga+blgb+clgc≥clga+algb+blgc alga+blgb+clgc=alga+blgb+clgc 上述三式相加得： 3（alga+blgb+clgc）≥（a+b+c）（lga+lgb+lgc） 即lg（aabbcc）≥
故aabbcc≥（abc）
|
参考解析：
a+b+c3
【简答题】
[4/6]设a，b，c为正数，利用排序不等式证明a3+b3+c3≥3abc．
参考答案：
| 证明：不妨设a≥b≥c＞0，∴a2≥b2≥c2， 由排序原理：顺序和≥反序和，得： a3+b3≥a2b+b2a，b3+c3≥b2c+c2b，c3+a3≥a2c+c2a 三式相加得2（a3+b3+c3）≥a（b2+c2）+b（c2+a2）+c（a2+b2）． 又a2+b2≥2ab，b2+c2≥2bc，c2+a2≥2ca． 所以2（a3+b3+c3）≥6abc， ∴a3+b3+c3≥3abc． 当且仅当a=b=c时，等号成立． |
参考解析：
无
【简答题】
[5/6]设a1，a2，…，an为实数，证明：a1+a2+…+ann≤a21+a22+…+ a2nn．
参考答案：
| 证明：不妨设a1≤a2≤…≤an，则由排序原理得： a12+a22+…+an2=a1a1+a2a2+…+anan a12+a22+…+an2≤a1a2+a2a3+…+ana1 a12+a22+…+an2≤a1a3+a2a4+…+an-1a1+ana2 … a12+a22+…+an2≤a1an+a2a1+…+anan-1． 将上述n个式子相加，得：n（a12+a22+…+an2）≤（a1+a2+…+an）2， 上式两边除以n2，并开方可得：
|
参考解析：
a1+
a2+…+
ann
【简答题】
[6/6]若 【图片】， 【图片】， 【图片】，则 ( ) A． 【图片】 B． 【图片】 C． 【图片】 D．...
参考答案：
| A |
参考解析：
无
