
创建自己的小题库
搜索

平行射影题库
题数
673
考试分类
高中数学>平行射影
售价
¥25
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-平行射影
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/673]如图,点ABC都在⊙ O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为 ( ) A. 【图片】 B....
参考答案:
| D |
参考解析:
无
【简答题】

[2/673]如图,若△ACD~△ABC,则下列式子中成立的是( ) 【图片】 A.CD2=AD·DB B.AC2=AD·AB C...
参考答案:
| B |
参考解析:
无
【简答题】

[3/673]如图, 【图片】四点在同一圆上, 【图片】与 【图片】的延长线交于点 【图片】,点 【图片】在 【图片】的延长线上. 【图片】(1)若 【图片】, 【...
参考答案:
|
(1)
 ;(2)证明过程详见解析. ;(2)证明过程详见解析.
|
参考解析:
本题主要以圆为几何背景考查线线平行、相等的证明以及相似三角形的证明,考查学生的转化与化归能力.第一问,利用四点共圆得
 和
和
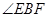 相等,再证明
相等,再证明
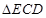 与
与
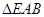 相似,得出边的比例关系,从而求出
相似,得出边的比例关系,从而求出
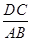 的值;第二问,利用已知
的值;第二问,利用已知
 得到边的关系,又因为
得到边的关系,又因为
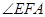 为公共角,所以得出
为公共角,所以得出
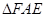 与
与
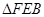 相似,从而得出
相似,从而得出
 与
与
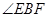 相等,根据四点共圆得与相等
相等,根据四点共圆得与相等
 与
与
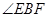 相等,通过转化角,得出
相等,通过转化角,得出
 与
与
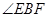 相等,从而证明两直线平行.
相等,从而证明两直线平行.
⑴
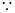
 四点共圆,
四点共圆,

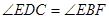 ,又
,又
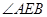 为公共角,
为公共角,
∴
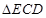 ∽
∽
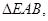 ∴
∴
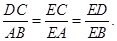
∴
 .
.
∴
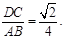 . 6分
. 6分
⑵
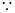
 ,
,
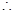
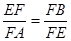 ,
,
又
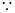
 ,
,
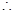
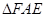 ∽
∽
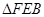 ,
,
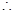
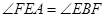 ,
,
又
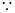
 四点共圆,
四点共圆,

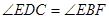 ,
,

 ,
,
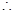
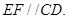 . 10分
. 10分
【简答题】

[4/673]如图,已知 【图片】的弦 【图片】交半径 【图片】于点 【图片】,若 【图片】, 【图片】,且 【图片】为 【图片】的中点,则 【图片】的长为&nbs...
参考答案:
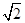
|
参考解析:
作出过C点的直径CD,根据D为OC的中点可以算出DE=3CD.因此设出CD长为x,DE长为3x,再用相交弦定理得到AD?BD=ED?CD,代入题中的数据可得x的值,即为CD的长.
解答:解: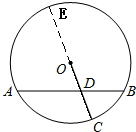 延长CO交圆O于E,则CE是圆O的直径
延长CO交圆O于E,则CE是圆O的直径
∵D为OC的中点,CE=2OC
∴CE=4CD?DE=3CD
设CD长为x,DE长为3x
根据相交弦定理,得AD?BD=ED?CD
∴3×2=x?3x=3x 2?x 2=2
∴x=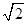 ,即CD=
,即CD=
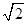
故答案为: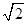
解答:解:
 延长CO交圆O于E,则CE是圆O的直径
延长CO交圆O于E,则CE是圆O的直径
∵D为OC的中点,CE=2OC
∴CE=4CD?DE=3CD
设CD长为x,DE长为3x
根据相交弦定理,得AD?BD=ED?CD
∴3×2=x?3x=3x 2?x 2=2
∴x=
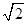 ,即CD=
,即CD=
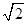
故答案为:
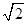
【简答题】

[5/673]如图,过圆 【图片】外一点 【图片】分别作圆的切线和割线交圆于 【图片】,且 【图片】, 【图片】是圆上一点使得 【图片】, 【图片】,则 【图片】_...
参考答案:
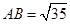
|
参考解析:
由弦切角定理得∠
PAB =∠
ACB , ∵∠
BAC =∠
APB , ∴△
PAB∽△
ACB ,∴则
 ,
,
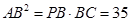 ,即
,即

 ,
,
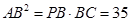 ,即
,即

【简答题】

[6/673]如图,圆 【图片】的割线 【图片】交圆 【图片】于 【图片】、 【图片】两点,割线 【图片】经过圆心.已知 【图片】, 【图片】, 【图片】.则圆 【...
参考答案:
|
8
|
参考解析:
由切割线定理,得:
 ,即6×
,即6×
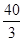 =(12-R)(12+R),解得R=8.
=(12-R)(12+R),解得R=8.
【简答题】

[7/673](几何证明选讲选做题)如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=________ 【图片】
参考答案:
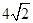
|
参考解析:
解由题意可知,在△ACD中,AC=4,AD=12,∠ACD=90°,∴DC=8
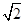 ∴cos∠D=
∴cos∠D=
 =
=

∵∠B=∠D,AE⊥BC,AB=6,∴cos∠B=
 ∴
∴
 =
=
 ,故答案为
,故答案为
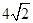 。
。
点评:解决该试题的关键是正确运用余弦函数,先在△ACD中计算cos∠D,再在△ABE中,计算cos∠B,即可得到结论.
【简答题】

[8/673]如图所示,⊙O是△ABC的内切圆,BC边上切点为D,AB=5,BC=7,AC=6,则BD=________. 【图片】
参考答案:
|
3
|
参考解析:
设E、F分别为AC、AB边上的切点,设BD=x,则CD=CE=7-x,AF=AE=6-(7-x)=x-1,BF=x,∴x-1+x=AB=5,∴x=3.
【简答题】

[9/673]如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若 【图片】= 【图片】, 【图片】= 【图片】,则 【图片】的值为______. ...
参考答案:
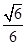
|
参考解析:
由题意可知△PBC∽△PDA,于是由
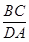 =
=
 =
=
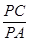 ,得
,得
 =
=
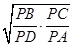 =
=
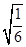 =
=
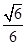 .
.
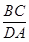 =
=
 =
=
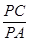 ,得
,得
 =
=
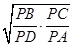 =
=
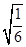 =
=
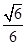 .
.
【简答题】

[10/673]如图所示,在圆的内接四边形ABCD中,AC平分∠BAD,EF切⊙O于C点,那么图中与∠DCF相等的角的个数是( ...
参考答案:
| B |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





