
创建自己的小题库
搜索

综合法与分析法题库
题数
229
考试分类
高中数学>综合法与分析法
售价
¥20
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-综合法与分析法
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/229]若P= 【图片】+ 【图片】,Q= 【图片】+ 【图片】(a≥0),则P,Q的大小关系是( ) A.P>QB.P=QC.P<QD.由a的取值确定
参考答案:
|
C
|
参考解析:
∵要证P<Q,只要证P
2<Q
2,
只要证:2a+7+2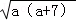 <2a+7+2
<2a+7+2
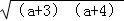 ,
,
只要证:a 2+7a<a 2+7a+12,
只要证:0<12,
∵0<12成立,
∴P<Q成立.
故选C
只要证:2a+7+2
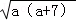 <2a+7+2
<2a+7+2
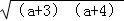 ,
,
只要证:a 2+7a<a 2+7a+12,
只要证:0<12,
∵0<12成立,
∴P<Q成立.
故选C
【简答题】

[2/229]用反证法证明命题“三角形的内角中至多有一个钝角”时,假设正确的是( ) A.三个内角中至少有一个钝角B.三个内角中至少有两个钝角C.三个内角...
参考答案:
|
B
|
参考解析:
反证法的第一步为否定结论,而原题中结论为三角形的内角中至多有一个钝角,即三角形的内角中有一个钝角或没有钝角,显然,其否定为三角形的内角中至少有两个钝角.
【简答题】

[3/229]已知数列{a n}中,S n是它的前n项和,并且S n+1=4a n+2(n=1,2,…),a 1=1. (1)设b n=a n+1-2a n(n=1...
参考答案:
|
(1)证明略(2)证明略(3){a
n}的前n项和公式为S
n=(3n-4)·2
n-1+2
|
参考解析:
(1)证明 ∵S
n+1=4a
n+2,
∴S n+2=4a n+1+2,两式相减,得
S n+2-S n+1=4a n+1-4a n(n=1,2,…),
即a n+2=4a n+1-4a n,
变形得a n+2-2a n+1=2(a n+1-2a n)
∵b n=a n+1-2a n(n=1,2,…),∴b n+1=2b n.
由此可知,数列{b n}是公比为2的等比数列.
(2)证明 由S 2=a 1+a 2=4a 1+2,a 1=1.
得a 2=5,b 1=a 2-2a 1=3.故b n=3·2 n-1.
∵c n= (n=1,2,…),
(n=1,2,…),
∴c n+1-c n=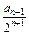 -
-
 =
=
 =
=
 .
.
将b n=3·2 n-1代入得
c n+1-c n= (n=1,2,…),
(n=1,2,…),
由此可知,数列{c n}是公差为 的等差数列,
的等差数列,
它的首项c 1=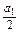 =
=
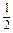 ,故c
n=
,故c
n=
 n-
n-
 (n=1,2,…).
(n=1,2,…).
(3)解 ∵c n= n-
n-
 =
=
 (3n-1).
(3n-1).
∴a n=2 n·c n=(3n-1)·2 n-2 (n=1,2,…)
当n≥2时,S n=4a n-1+2=(3n-4)·2 n-1+2.
由于S 1=a 1=1也适合于此公式,
所以{a n}的前n项和公式为S n=(3n-4)·2 n-1+2.
∴S n+2=4a n+1+2,两式相减,得
S n+2-S n+1=4a n+1-4a n(n=1,2,…),
即a n+2=4a n+1-4a n,
变形得a n+2-2a n+1=2(a n+1-2a n)
∵b n=a n+1-2a n(n=1,2,…),∴b n+1=2b n.
由此可知,数列{b n}是公比为2的等比数列.
(2)证明 由S 2=a 1+a 2=4a 1+2,a 1=1.
得a 2=5,b 1=a 2-2a 1=3.故b n=3·2 n-1.
∵c n=
 (n=1,2,…),
(n=1,2,…),
∴c n+1-c n=
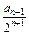 -
-
 =
=
 =
=
 .
.
将b n=3·2 n-1代入得
c n+1-c n=
 (n=1,2,…),
(n=1,2,…),
由此可知,数列{c n}是公差为
 的等差数列,
的等差数列,
它的首项c 1=
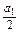 =
=
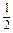 ,故c
n=
,故c
n=
 n-
n-
 (n=1,2,…).
(n=1,2,…).
(3)解 ∵c n=
 n-
n-
 =
=
 (3n-1).
(3n-1).
∴a n=2 n·c n=(3n-1)·2 n-2 (n=1,2,…)
当n≥2时,S n=4a n-1+2=(3n-4)·2 n-1+2.
由于S 1=a 1=1也适合于此公式,
所以{a n}的前n项和公式为S n=(3n-4)·2 n-1+2.
【简答题】

[4/229]用反证法证明命题“三角形的内角至多有一个钝角”时,假设正确的是( ) A.假设至少有一个钝角B.假设至少有两个钝角C.假设没有一个钝角D.假设没有一个...
参考答案:
|
B
|
参考解析:
注意到:“至多有一个”的否定应为: “至少有两个”知需选B.
【简答题】

[5/229]求证: 【图片】
参考答案:
|
同解析。
|
参考解析:

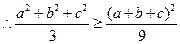
即

【简答题】

[6/229]用反证法证明命题“若 【图片】,则 【图片】、 【图片】全为0( 【图片】、 【图片】 【图片】)”,其反设正确的 A 【图片】、 【图片】至少有一不...
参考答案:
|
A
|
参考解析:
无
【简答题】

[7/229]证明不等式 【图片】的最适合的方法是( ) A.综合法 B.分析法 C.间接证法 D.合情推理法
参考答案:
| B |
参考解析:
无
【简答题】

[8/229]设 【图片】, 【图片】,并且对于任意 【图片】, 【图片】成立. 猜想 【图片】的表达式为 A. 【图片】B. 【图片】C. 【图片】D. 【图片】
参考答案:
|
B
|
参考解析:
令
 ,则
,则
 ,而
,而
 ,
,
 ,而令
,而令
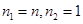 得
得
 ,联想等比数列,猜想
,联想等比数列,猜想
 ,故选择B
,故选择B
【简答题】

[9/229]设 【图片】为正整数,且 【图片】与 【图片】皆为完全平方数,对于以下两个命题: 【图片】(甲). 【图片】必为合数;(乙). 【图片】必为两个平方数...
参考答案:
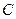
|
参考解析:
:设
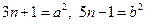 ,
,
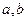 为正整数;则
为正整数;则
 …1,
…1,
由此知,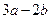 为正整数,且
为正整数,且
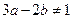 ,因为若
,因为若
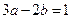 ,则
,则
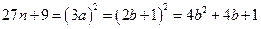 ,即
,即
 ,则
,则
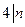 ,记
,记
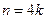 ,得
,得
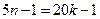 不为平方数,矛盾!所以
不为平方数,矛盾!所以
 ,故由1得,
,故由1得,
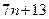 为合数;又因为
为合数;又因为
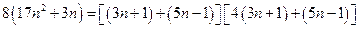
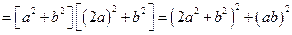 ,故选
,故选
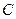 .(例如
.(例如
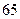 是上述
是上述
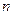 之一).
之一).
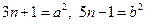 ,
,
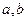 为正整数;则
为正整数;则
 …1,
…1,
由此知,
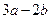 为正整数,且
为正整数,且
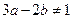 ,因为若
,因为若
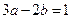 ,则
,则
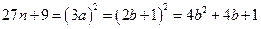 ,即
,即
 ,则
,则
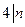 ,记
,记
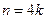 ,得
,得
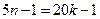 不为平方数,矛盾!所以
不为平方数,矛盾!所以
 ,故由1得,
,故由1得,
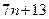 为合数;又因为
为合数;又因为
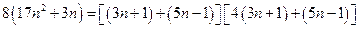
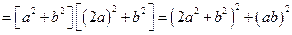 ,故选
,故选
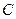 .(例如
.(例如
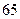 是上述
是上述
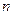 之一).
之一).
【简答题】

[10/229]用反证法证明命题“若 【图片】都是正数,则 【图片】三数中至少有一个不小于 【图片】”,提出的假设是( ...
参考答案:
|
D
|
参考解析:
根据反证法的思路可知,将结论变为否定来加以证明,即“若
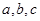 都是正数,则
都是正数,则
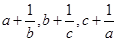 三数中至少有一个不小于
三数中至少有一个不小于
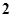 ”,提出的假设为
”,提出的假设为
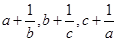 都小于2,选D.
都小于2,选D.
点评:本题主要考查求一个命题的否定,用反证法证明数学命题,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于基础题.

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





