
创建自己的小题库
搜索

匀变速直线运动规律的应用题库
题数
916
考试分类
高中物理>匀变速直线运动规律的应用
售价
¥25
 手机预览
手机预览
收藏
分享
去刷题
简介
高中物理-匀变速直线运动规律的应用
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/916]一物体以一定的初速度,沿倾角可在0-90°之间任意调整的木板向上滑动,设它沿木板向上能达到的最大位移为x.若木板倾角不同时对应的最大位移x与木板倾角α...
参考答案:
| (1)当α=90°时,x=1.25m,物体做竖直上抛运动,根据动能定理,有: mgx=
解得:v0=
(2)当α=30°时,x=1.25m 根据速度位移关系公式,有: a=
根据牛顿第二定律,有: a=g(sin30°+μcos30°) 联立解得:μ=
(3)当α=60°时,根据牛顿第二定律,有: a1=g(sin60°+μcos60°)=
根据速度位移关系公式,有: x=
答:(1)物体初速度的大小为5m/s. (2)物体与木板间的动摩擦因数为
(3)当α=60°时,它沿木板向上能达到的最大位移为x为1.0825m. |
参考解析:
无
【简答题】

[2/916](15分)如图13所示,倾角为30°的光滑斜面体,固定在地面上。质量为m的物块在一平行于斜面向上的力 F作用下,从斜面底端由静止出发经一段时间 t到达...
参考答案:
|
解:设斜面长为
l,物体受拉力
F作用时的加速度为
a
1,不受拉力
F作用时的加速度为
a
2,则有:
当力 F一直作用时有: 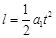 (2分) (2分)
力 F只作用一半时间有:  , ,
 (3分) (3分)
又 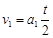 ,
l
1+
l
2=
l (2分) ,
l
1+
l
2=
l (2分)
由以上五式可解得: a 1=4 a 2(2分) 由牛顿第二定律,受拉力 F时有: F- mgsin30°= ma 1 (2分) 不受拉力 F时有: mgsin30°= ma 2 (2分) 解得: 
所以物块所受拉力 F与重力 mg的比值为5∶2。(2分) |
参考解析:
无
【简答题】

[3/916]一辆卡车,它急刹车时的加速度的大小是5m/s2,如果要求它在急刹车后22.5m内必须停下,假设卡车刹车过程做的是匀减速直线运动。求: (1)它的行驶速...
参考答案:
解:(1)根据运动学公式: ∴  , ,  (2)  (3)  |
参考解析:
无
【简答题】

[4/916]汽车原来以12m/s的速度沿平直公路行驶,刹车后获得的加速度大小为3 【图片】。则:(1)刹车后经5 s汽车将滑行多远?(2)汽车在停止前2 s内滑行...
参考答案:
解:(1)汽车滑行的总时间 由  ,得 ,得 (2)汽车在停止前2 s内滑行的距离  |
参考解析:
无
【简答题】

[5/916]做匀加速直线运动的物体,速度从 v增加到2 v时经过的位移是x,则它的速度从3 v增加到4 v时所发生的位移是( ) A. 【图片】B. 【图片】C....
参考答案:
|
D
|
参考解析:
根据速度位移公式可得
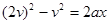 ,即
,即
 ;
;
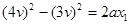 ,即
,即
 ;两式对比可得
;两式对比可得
 ,故选D,
,故选D,
点评:在使用位移速度公式的时候需要正确区分物体运动的始末速度,比较简单
【简答题】

[6/916]如图所示,一平板车以某一速度v0=5 m/s匀速行驶,某时刻一货箱(可视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l= 【图片】 m,货箱...
参考答案:
| 解:(1)货箱放到车上后,先做匀加速运动,设经过时间t和车达到相同速度,此时货箱和车的位移分别为x1、x2 对货箱:μmg=ma1,a1t =v0-at,x1=v0t-  a1t2 a1t2对平板车:x2=v0t-  at2 at2此时,货箱相对车向后移动了△x=x2-x1=2.5 m<l=  m,故货箱不会从车后端掉下来 m,故货箱不会从车后端掉下来(2)由于货箱的最大加速度a1=μg=2 m/s2<a,所以二者达到相同速度后,分别以不同的加速度匀减速运动到停止,此时相同速度为v=a1t=2 m/s 对货箱:s1=v2/2a1=1 m 对平板车:s2=v2/2a=2/3 m 故货箱到车尾的距离d1=l-△x+s1-s2=1 m (3)设经过时间t1货箱和车分离,由位移关系得:d1=  a2t12- a2t12- a1t12 a1t12 解得t1=1 s 分离时货箱速度v1=a1t1=2 m/s,货箱做平抛运动,经过时间t2落地 ∴h=  gt22,得t2=0.5 s gt22,得t2=0.5 s 则在平板车启动的t3=3 s内,货箱的水平位移x1'=  a1t12+v1t2=2 m a1t12+v1t2=2 m平板车的位移为:x2'=  a2t32=18 m a2t32=18 m故货箱离平板车后端的距离:d2=x2'-x1'-d1=15 m |
参考解析:
无
【简答题】

[7/916]汽车以v 0=10m/s的速度在水平路面上匀速运动,刹车2s后它的速度降为6m/s。求: (1)刹车过程中的加速度; (2)刹车后经多长时间汽车停下;...
参考答案:
|
(1)
 (2) (2)
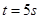 (3) (3)

|
参考解析:
(1)由运动学公式可得:
 ①(2分)
①(2分)
将数据代入①式可解得:
 ②(1分)
②(1分)
(2)汽车停车所需时间t,由运动学公式可得:
 ③(2分)
③(2分)
由③式可解得:
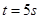 ④(1分)
④(1分)
(3)汽车从刹车到停下所通过的位移是s,则:
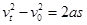 ⑤(2分)
⑤(2分)
由⑤式可解得:
 (1分)
(1分)
点评:在分析汽车刹车问题时,不能一味的带公式,需要先判断汽车静止所用的时间,跟题目中时间对比,
【简答题】

[8/916]汽车进站关闭发动机做匀减速直线运动,当滑行x1=30m时,速度恰好减为初速度的一半,接着又滑行了t2=20s才停止。求:汽车关闭发动机时的速度v0和滑...
参考答案:
解:   解得    |
参考解析:
无
【简答题】

[9/916]一辆摩托车能达到最大速度为30m/s,要想在3min内由静止起沿一条平直公路追上前面1000m处正以20m/s的速度匀速行驶的汽车,则摩托车必须以多大...
参考答案:
| 设摩托车加速时间为t,加速度为a,3min=180s 则可列 at=v1 ①
代入数据 解得 a=0.56m/s2 答:摩托车必须以0.56m/s2的加速度起动 |
参考解析:
12
【简答题】

[10/916]足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中。某足球场长90m、宽60m。攻方前锋在中线处将足球沿边...
参考答案:
解:(1)已知足球的初速度为 ,加速度大小为 ,加速度大小为 足球做匀减速运动的时间为:  运动位移为:  (2)已知前锋队员的加速度为  ,最大速度为 ,最大速度为 ,前锋队员做匀加速运动达到最大速度的时间和位移分别为: ,前锋队员做匀加速运动达到最大速度的时间和位移分别为:   之后前锋队员做匀速直线运动,到足球停止运动时,其位移为:  由于  ,故足球停止运动时,前锋队员没有追上足球,然后前锋队员继续以最大速度匀速运动追赶足球利用公式 ,故足球停止运动时,前锋队员没有追上足球,然后前锋队员继续以最大速度匀速运动追赶足球利用公式 ,得 ,得 前锋队员追上足球的时间  (3)此时足球距底线的距离为:  ,速度为v3=10m/s ,速度为v3=10m/s 足球运动到停止的位移为:  所以,足球运动到底线时没停 由公式  ,足球运动到底线的时间为:t4=1 s ,足球运动到底线的时间为:t4=1 s前锋队员在这段时间内匀速运动的位移:  所以前锋队员不能在底线前追上足球 |
参考解析:
无

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





