
创建自己的小题库
搜索

二项式定理与性质题库
题数
2000
考试分类
高中数学>二项式定理与性质
售价
¥30
 手机预览
手机预览
收藏
分享
去刷题
简介
高中数学-二项式定理与性质
...更多



0道

0道

0道



章节目录
题目预览(可预览10题)
【简答题】

[1/2000]已知a= 【图片】,则(x- 【图片】)的展开式中的常数项为( )
参考答案:
- |
参考解析:
无
【简答题】

[2/2000]求和:1-C1013+C10232-C10333+…+C1010310=______.
参考答案:
| 由二项式定理可知:1-C1013+C10232-C10333+…+C1010310=(1-3)10=210=1024. 故答案为:1024. |
参考解析:
无
【简答题】

[3/2000]已知(x+12• 4x)n的展开式前三项中的x的系数成等差数列.(1)展开式中所有的x的有理项为第几项?(2)求展开式中系数最大的项.
参考答案:
| (1)因为展开式前三项中的x的系数成等差数列, 所以2•
所以n=8或n=1(舍去), n=8时,展开式的通项公式为Tr+1=
由题意,4-
∴r=0,4,8, ∴展开式中所有的x的有理项为第1,5,9项; (2)设第r+1项为系数最大的项,则由
|
参考解析:
无
【简答题】

[4/2000]二项式 【图片】的展开式中常数项的值为( )。
参考答案:
| 20 |
参考解析:
无
【简答题】

[5/2000]883+6被49除所得的余数是( ) A.0B.14C.-14D.35
参考答案:
| 由二项式定理展开得883+6=(7+1)83+6 =783+
=72M+83×7+7(M是正整数) =49M+49×12 =49N.(N是正整数). ∴883+6被49除所得的余数是0. 故选A. |
参考解析:
C183
【简答题】

[6/2000]若 【图片】,则 【图片】的值为( ) A. 【图片】B. 【图片】C.0D.2
参考答案:
|
B
|
参考解析:
解:因为
 ,对x令值为
,对x令值为
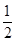 ,可知
,可知
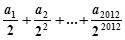 为-1,选B
为-1,选B
 ,对x令值为
,对x令值为
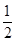 ,可知
,可知
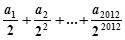 为-1,选B
为-1,选B
【简答题】

[7/2000](本小题满分12分) 已知 【图片】展开式中最后三项的系数的和是方程 【图片】的正数解,它的中间项是 【图片】,求 【图片】的值.
参考答案:
|
解:由
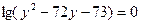 得 得
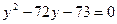 , ,
∴  (舍去)或 (舍去)或
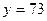

 ………2分 ………2分
由题意知,  ,∴ ,∴
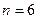 … …
 ……5分 ……5分
已知条件知,其展开式的中间项为第4项, 即 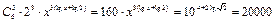 , ………8分 , ………8分
∴ 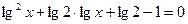 , ………10分 , ………10分
∴ 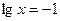 或 或
 ,∴ ,∴
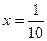 或 或
 . ………12分 . ………12分
|
参考解析:
略
【简答题】

[8/2000]若(x- 【图片】)n的展开式中第3项的二项式系数是15,则展开式中所有项系数之和为 [ ] A. 【...
参考答案:
| B |
参考解析:
无
【简答题】

[9/2000]【图片】若二项式 【图片】的开展式中的常数项为 【图片】则 【图片】 ...
参考答案:
|
6
|
参考解析:
略
【简答题】

[10/2000]已知 【图片】n展开式中的二项式系数的和比(3a+2b) 7展开式的二项式系数的和大128,求 【图片】n展开式中的系数最大的项和系数最小的项.
参考答案:
|
最大的项T
5=70x
4;系数最小的项T
4=-56x
7,T
6=-56x
|
参考解析:
2
n-2
7=128,n=8,
 8的通项T
r
+1=
8的通项T
r
+1=
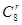 (x
2)
8
-r
(x
2)
8
-r
 r=(-1)
r
r=(-1)
r
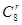 x
16
-3r,
x
16
-3r,
当r=4时,展开式中的系数最大,即T 5=70x 4为展开式中的系数最大的项;
当r=3,或5时,展开式中的系数最小,即T 4=-56x 7,T 6=-56x为展开式中的系数最小的项
 8的通项T
r
+1=
8的通项T
r
+1=
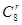 (x
2)
8
-r
(x
2)
8
-r
 r=(-1)
r
r=(-1)
r
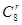 x
16
-3r,
x
16
-3r,
当r=4时,展开式中的系数最大,即T 5=70x 4为展开式中的系数最大的项;
当r=3,或5时,展开式中的系数最小,即T 4=-56x 7,T 6=-56x为展开式中的系数最小的项

 复制链接
复制链接 新浪微博
新浪微博 分享QQ
分享QQ 微信扫一扫
微信扫一扫





