创建自己的小题库
搜索
抛物线的性质（顶点、范围、对称性、离心率）题库
题数
867
考试分类
高中数学>抛物线的性质（顶点、范围、对称性、离心率）
售价
¥25
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-抛物线的性质（顶点、范围、对称性、离心率）
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/867]两个顶点在抛物线y2=2px（p＞0）上，另一个顶点是此抛物线焦点，这样的正三角形有（ ） A．4个 B．3个 C．2个 D．1个
参考答案：
| C |
参考解析：
无
【简答题】
[2/867]抛物线y2=2x上的两点A、B到焦点F的距离之和是5，则线段AB的中点M的横坐标是______．
参考答案：
| ∵F是抛物线y2=2x的焦点 F（
设A（x1，y1） B（x2，y2） ∴|AF|+|BF|=x1+
解得x1+x2=4 ∴线段AB的中点横坐标为：2． 故答案为：2． |
参考解析：
12
【简答题】
[3/867]已知A，B是抛物线y2=-7x上的两点，且OA⊥OB（Ⅰ）求证：直线AB过定点，并求出定点坐标；（Ⅱ）求△AOB的面积的最小值．
参考答案：
（1）证明：设A（x1，y1），B（x2，y2），则
∵OA⊥OB，∴
∴x1x2+y1y2=0， ∴（-
∴y1y2=-49，x1x2=49， ∴kAB=
∴AB的方程为y-y1=
∴y=
∴y=
∴直线AB过点（-7，0）…（6分） （2）∵直线AB过点（-7，0），OA⊥OB， ∴当直线AB过（-7，0）且垂直于x轴时，△AOB的面积的取最小值． 此时A（-7，7），B（-7，-7）， ∴|OA|=|OB|=7
∴△AOB的面积的最小值S=
|
参考解析：
| y12=-7x1 |
| y22=-7x2 |
【简答题】
[4/867]AB为过抛物线焦点F的弦，P为AB中点，A、B、P在准线l上射影分别为M、N、Q，则下列命题：①以AB为直径作圆则此圆与准线l相交；②MF⊥NF；③A...
参考答案：
| 由题意，AP+BP=AM+BN ∴PQ=
由AP=AF可知∠AMF=∠AFM，同理∠BFN=∠BNF，利用AM∥BN，可得MF⊥NF，从而②④正确； 对于 ⑤，不妨设抛物线方程为y2=2px，直线AB：x=ky+
联立可得y2-2kpy-p2=0 设A(
∴kOA=
∵y1y2=-p2，∴kOA=kON，故⑤正确 故答案为②③④⑤ |
参考解析：
12
【简答题】
[5/867]已知点A（0，2）抛物线y2=2px（p＞0）的焦点为F，准线为l，线段FA交抛物线与点B，过B做l的垂线，垂足为M，若AM⊥MF，则p=（ ...
参考答案：
 |
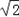参考解析：
无
【简答题】
[6/867]如果抛物线y2=ax的准线是直线x=-1，那么它的焦点坐标为（ ） A．（1，0） B．（2，0） C．（3，0） D．（-1，0）
参考答案：
| A |
参考解析：
无
【简答题】
[7/867]抛物线y= 【图片】x2的焦点坐标是（ ） A．( 【图片】，0) B．（1，0） C．（0，2） D．（0，1）
参考答案：
| D |
参考解析：
无
【简答题】
[8/867]过抛物线y2=2px（p＞0）的焦点作倾斜角为45°的直线交抛物线于A，B两点，若线段AB的中点坐标为（3，2），则p的值为（ ） A．12B．1C...
参考答案：
∵抛物线y2=2px的焦点为F（
∴过焦点且倾斜角为45°的直线l方程为y=x-
与抛物线方程消去x，得
设A（x1，y1），B（x2，y2）， 可得y1+y2=2p=2×2=4，解之得p=2 故选：C |
参考解析：
p2
【简答题】
[9/867]已知抛物线y2=4x上一点到焦点的距离为5，这点的坐标为______．
参考答案：
| ∵抛物线方程为y2=4x， ∴焦点为F（1，0），准线为l：x=-1 设所求点坐标为P（x，y） 作PQ⊥l于Q 根据抛物线定义可知P到准线的距离等于P、Q的距离 即x+1=5，解之得x=4， 代入抛物线方程求得y=±4 故点P坐标为：（4，±4） 故答案为：（4，4）或（4，-4）．  |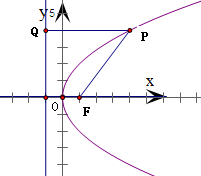
参考解析：
无
【简答题】
[10/867]已知抛物线y2=4x与直线y=2x+b相交于A，B两点，|AB|=35．（1）求b的值；（2）设P 是x轴上的一点，当△PAB的面积为39时...
参考答案：
| （1）设A（x1，y1）、B（x2，y2）， 由抛物线y2=4x与直线y=2x+b，可得4x2+4（b-1）x+b2=0， △=16（b-1）2-16b2＞0，∴b＜
又由韦达定理有x1+x2=1-b，x1x2=
∴|AB|=
即
（2）设x轴上点P（x，0），P到AB的距离为d，则 d=
∴S△PBC=
∴|2x-4|=26， ∴x=15或x=-11， ∴P（15，0）或（-11，0）． |
参考解析：
12
