创建自己的小题库
搜索
匀变速直线运动的位移与时间的关系题库
题数
1720
考试分类
高中物理>匀变速直线运动的位移与时间的关系
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中物理-匀变速直线运动的位移与时间的关系
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/1720]一物体由静止开始作匀加速运动，它在第n秒内的位移是s，则其加速度大小为 [ ] A． 【图片】 B． ...
参考答案：
| A |
参考解析：
无
【简答题】
[2/1720]如图所示，一质量M=2.0kg的长木板静止放在光滑水平面上，在木板的右端放一质量m=1.0kg可看作质点的小物块，小物块与木板间的动摩擦因数为μ=0....
参考答案：
| （1）设小物块受到的摩擦力为f=μN1=μmg=0.2×1.0×10N=2N 方向水平向右． （2）设小物块的加速度为a1，木板在恒力F作用下做匀加速直线运动时的加速度为a2，此过程中小物块的位移为s1，木板的位移为s2则 由牛顿定律及运动规律可知：f=ma1 a1=2.0m/s2 s1=
s2=
s2-s1=l 带入数据解得：a2=4m/s2 设木板受到的摩擦力为f’，f’=f，对木板根据牛顿第二定律：F-f’=Ma2， 则F=f’+ma2，代入数值得出F=10N． （3）设撤去F时小物块和木板的速度分别为v1和v2，撤去F后，木板与小物块组成的系统动量守恒， 当小物块与木板相对静止时，它们具有共同速度v，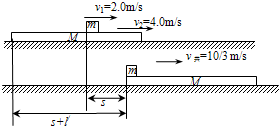 
根据动量守恒定律得：mv1+Mv2=（m+M）v v=
对小物块：根据动能定理：fs=
对木板：根据动能定理：-f（s+l′）=
代入数据：l′=
所以木板的长度至少为L=l+l′=
答：（1）小物块在加速过程中受到的摩擦力的大小为2N，方向水平向右；（2）作用于木板的恒力F的大小为10N；（3）木板的长度至少是1.7m． |
参考解析：
无
【简答题】
[3/1720]质量为0.5kg的物体静止在水平面上，受到一个大小为3N的水平拉力F作用后开始运动，运动中所受滑动摩擦阻力为2N，此拉力F作用力2s后，其大小变为1N...
参考答案：
| （1）根据牛顿第二定律得： 当拉力为3N时的加速度a1=
当拉力为1N时的加速度a1=
2s末的速度v1=a1t=4m/s 改变拉力后的时间t2=
（2）匀加速运动的位移x1=
匀减速运动的位移x2=-
所以总位移为8m （3）全过程中拉力F对物体所做的总功W=F1x1+F2x2=3×4+1×4=16J （4）2s末的速度最大，力F也最大，所以拉力F的最大功率P=Fv=3×4=12W 答：（1）物体在改变拉力大小后，还能运动2s； （2）物体总位移为8m； （3）全过程中拉力F对物体所做的总功为16J； （4）拉力F的最大功率为12W． |
参考解析：
无
【简答题】
[4/1720]一物体做匀加速直线运动，初速度为0.5m/s，加速度是2m/s2．则它在第2秒内的位移是______m．
参考答案：
物体在第2s内的位移x=(v0t1+
故答案为：3.5m． |
参考解析：
无
【简答题】
[5/1720]甲、乙两辆汽车速度相等，在同时制动后，设均做匀减速直线运动，甲经3s停止，共前进了36m，乙经1.5s停止，则乙车前进的距离是______．
参考答案：
对于甲车，x=
对于乙车，x′=
故答案为：18m． |
参考解析：
v0+02
【简答题】
[6/1720]汽车从静止开始以a=1m/s2的加速度前进，某人在车后s0=25m处同时开始以6m/s的速度匀速追汽车．（1）经过多长时间汽车的速度达到6m/s；（2...
参考答案：
| （1）设车历时t其速度达到v1=6m/s， 则有t=
t=6s． （2）在t=6s之前，人的速度大于车的速度，人逐渐靠近车，t=6s之后，人的速度小于车的速度，人逐渐远离车， 在t=6s时，人车之间的距离为最近，若此时人未追上车就再也追不上车了． t时间内 s人=v1t s人=36m s车=
s车=18m s车+s0=18+25m=43m s人小于（s车+s0），可见人追不上． （3）t=6s时，人车距离最近，△s=s车+s0-s人 △s=（18+25-36）m=7m． 答：（1）经过6s汽车的速度达到6m/s； （2）不能追上； （3）人、车间的最小距离为7m． |
参考解析：
v1a
【简答题】
[7/1720]如图甲所示，质量m=1.0kg的物体置于倾角θ=37°的固定粗糙斜面上，t=0时对物体施以平行于斜面向上的拉力F，t1=1s时撤去拉力，物体运动的部分...
参考答案：
| 由图象可知，撤去拉力前后物体的加速度大小分别为 a1=
根据牛顿第二定律得 F-μmgcosθ-mgsinθ=ma1 mgsinθ+μmgcosθ=ma2 得F=m（a1+a2）=1×1×（20+10）N=30N 撤去F前物体上滑的距离S1=
S2=
所以H=（s1+s2）sinθ=18m 答：拉力F的大小为30N，物块能上升的最大高度为18m． |
参考解析：
△v△t
【简答题】
[8/1720]某物体做直线运动，遵循的运动方程为x=6t-t2（其中，x单位为m，t单位为s）．则该物体在0～4s时间内经过的路程为（ ） A．8m B．9m C...
参考答案：
| C |
参考解析：
无
【简答题】
[9/1720]物体的位移随时间变化的函数关系是x=4t-2t2（m），则该物体在2s内发生位移是（ ） A．0B．1mC．2mD．4m
参考答案：
| 将t=2s代入x=4t-2t2（m）得： x=4×2-2×22=0 故选：A |
参考解析：
无
【简答题】
[10/1720]一个向正东方向做匀变速直线运动的物体，在第3s内发生的位移为8m，在第4s内发生的位移为5m，则关于物体运动加速度的描述正确的是（ ） A．大小为3...
参考答案：
| 由题意，物体做匀变速直线运动，已知第3s内发生的位移为 x1=8m，在第4s内发生的位移为 x2=5m，两段相等的时间为t=1s． 根据匀变速直线运动的推论：△x=aT2，得：x2-x1=at2， 则得 a=
故选：B． |
参考解析：
x2-
x1
t2
