创建自己的小题库
搜索
简单线性规划问题（用平面区域表示二元一次不等式组）题库
题数
2000
考试分类
高中数学>简单线性规划问题（用平面区域表示二元一次不等式组）
售价
¥30
手机预览
收藏
分享
复制链接
新浪微博
分享QQ
微信扫一扫
复制链接新浪微博分享QQ微信扫一扫去刷题
简介
高中数学-简单线性规划问题（用平面区域表示二元一次不等式组）
...更多
0道
0道
0道
章节目录
题目预览(可预览10题)
【简答题】
[1/2000]已知点P（3，-1）和Q（-1，2）在直线ax+2y=1的同侧，则实数a的取值范围是（ ） A．（1，3）B．（-∞，1）∪（3，+∞）C．（-∞，...
参考答案：
| 点A（3，-1），B（-1，2）在直线ax+2y-1=0的同侧， （3a-2-1）（-a+4-1）＞0 解不等式可得，1＜a＜3 故选A． |
参考解析：
无
【简答题】
[2/2000]已知两定点A（-2，0），B（1，0），动点P（x，y）满足|PA|=2|PB|．（1）求动点P的轨迹C的方程；（2）求yx+2的取值范围；（3）设点...
参考答案：
 （1）已知两定点A（-2，0），B（1，0），如果动点P满足|PA|=2|PB|，设P点的坐标为（x，y）， 则（x+2）2+y2=4[（x-1）2+y2]，即（x-2）2+y2=4， 所以点的轨迹是以（2，0）为圆心，2为半径的圆， （2）
而点P（x，y）在圆（x-2）2+y2=4，上运动， 设
d=
结合图形易求得
（3）①如图，由题意知直线MN可看成是以SC为直径的圆与圆C的公共弦所在的直线， 设S（-2，t），C（2，0），则以SC为直径的圆的方程为： x2+（y-
两者作差，得：4x-ty-4=0，此方程即为直线MN的方程， 令y=0得x=1，即直线MN过点B（1，0）， 从而M，B，N三点共线； ②
=|
=(SC2-MC2) (1-2×
设SC=m，由于MC=2，且m≥4， ∴
当且仅当m=4时，它取得最小值，最小值为：m2+
故
|
参考解析：
yx+2
【简答题】
[3/2000]已知变量x，y满足关系式
参考答案：
| 作出不等式组表示的平面区域，如图所示的阴影部分 由于z=x2+（y+1）2的几何意义是平面区域内的点P（x，y）与定点M（0，-1）的距离的平方 结合图形可知，MC为距离的最大值，由 |
参考解析：
无
【简答题】
[4/2000]曲线f（x）= 【图片】（其中e为自然对数的底数）在点（0,1）处的切线与直线y=－x+3和x轴所围成的区域为D（包含边界），点P（x，y）为区域D内...
参考答案：
|
A
|
参考解析：
，切线的斜率k=
=1，切线方程为y=x+1，区域D如图所示，目标函数z=x-3y过点（3,0）时，z的值最大，最大值为3-3×0=3，故选A.
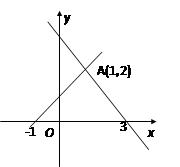
【简答题】
[5/2000]已知变量x，y满足约束条件2x-y≤0x-2y+3≥0x≥0，则目标函数z=x+y的最大值为______．
参考答案：
满足约束条件
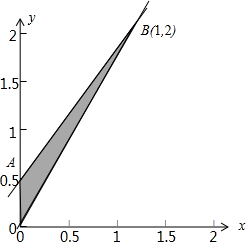 ∵目标函数z=x+y ∴zO=0+0=0， zA=0+0.5=0.5， zB=1+2=3， 故目标函数z=x+y的最大值为3 故答案为：3 |
参考解析：
无
【简答题】
[6/2000]已知实数 【图片】满足 【图片】，且目标函数 【图片】的最大值为6，最小值为1，其中 【图片】的值为（ ） A．4B．3C．2D...
参考答案：
|
A.
|
参考解析：
由题意可得下图，由图知直线
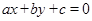通过A，B两点，即
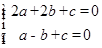，解得
.
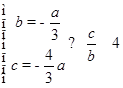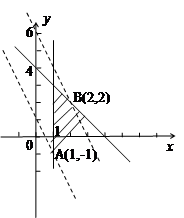
【简答题】
[7/2000]已知变量x,y满足约束条件 【图片】，则z=x+2y的最小值为 A．3B．1C．-5D．-6
参考答案：
|
C
|
参考解析：
画出平面区域可知,当目标函数z=x+2y表示的直线经过点
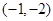时, z=x+2y取得最小值为
,故选C.
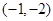时, z=x+2y取得最小值为
,故选C.
【简答题】
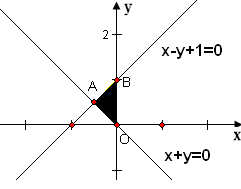
[8/2000]若实数 【图片】满足 【图片】则 【图片】的最大值是( ) A．0B． 【图片】C． 2D．3
参考答案：
|
D
|
参考解析：
作出如右图所示的可行域，则当直线z=2x+3y经过点B(0,1)时，z取得最大值，最大值为3,故应选D.
【简答题】
[9/2000]若 x≤2 y≤2 x+y≥2 ，则目标函数z=x2+y2的取值范围是（ ） A．[2，2 2] B．[ 2，2 2] C．[2，8] D．[ 2，...
参考答案：
解：由 ，作出可行域： ∵A（0，2），∴ZA =0+4=4， ∵B（2，0），∴ZB=4+0=4， ∵C（2，2），∴ZC=4+4=8， ∵目标函数z=x2+y2是可行域内的点与原点距离的平方， 原点（0，0）到直线x+y=2的距离  ， ∴目标函数z=x2+y2的取值范围是[2，8]． 故选C．  |
参考解析：
无
【简答题】
[10/2000]设关于x，y的不等式组2x-y+1＞0 ， x+m＜0 ， y-m＞0表示的平面区域内...
参考答案：
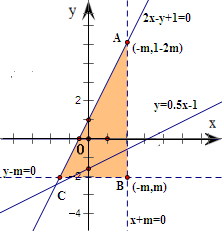 先根据约束条件
要使可行域存在，必有m＜-2m+1，要求可行域包含直线y=
在直线y=
故得不等式组
解之得：m＜-
故选C． |
参考解析：
无
